


Next: Ideals and minimal characteristic
Up: Linear recursive sequences
Previous: Linear recursive sequences
Characteristic polynomials
The characteristic polynomial of a linear recurrence
is defined to be the polynomial
For example, the characteristic polynomial of
the recurrence
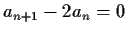 satisfied by the sequence (1)
is
satisfied by the sequence (1)
is 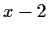 .
.
Here is another example: the famous Fibonacci sequence
which can be described by the starting values 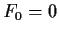 ,
, 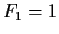 and the recurrence relation
and the recurrence relation
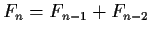 for all for all 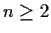 . . |
(3) |
To find the characteristic polynomial, we first need to
rewrite the recurrence relation in the form (2).
The relation (3) is equivalent to
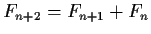 for all for all 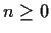 . . |
(4) |
Rewriting it as
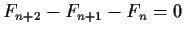 |
(5) |
shows that 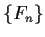 is a linear recursive sequence satisfying
a recurrence of order 2,
with
is a linear recursive sequence satisfying
a recurrence of order 2,
with 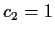 ,
, 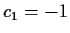 , and
, and 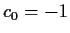 .
The characteristic polynomial is
.
The characteristic polynomial is 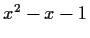 .
.



Next: Ideals and minimal characteristic
Up: Linear recursive sequences
Previous: Linear recursive sequences
Zvezdelina Stankova-Frenkel
2000-09-20