


Next: Recursive definitions
Up: Linear recursive sequences
Previous: Linear recursive sequences
Sequences
A sequence is an infinite list of numbers, like
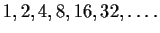 |
(1) |
The numbers in the sequence are called its terms.
The general form of a sequence is
where 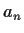 is the
is the 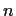 -th term of the sequence.
In the example (1) above,
-th term of the sequence.
In the example (1) above, 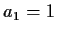 ,
, 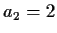 ,
, 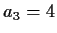 , and so on.
, and so on.
The notations 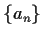 or
or
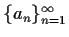 are abbreviations for
are abbreviations for
Occasionally the indexing of the terms will start with something other
than 1. For example,
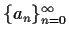 would mean
(In this case
would mean
(In this case 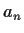 would be the
would be the 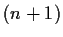 -st term.)
-st term.)
For some sequences, it is possible to give an explicit formula
for 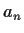 : this means that
: this means that 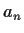 is expressed as a function of
is expressed as a function of 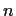 .
For instance, the sequence (1) above can be described by
the explicit formula
.
For instance, the sequence (1) above can be described by
the explicit formula
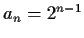 .
.
Zvezdelina Stankova-Frenkel
2000-09-20
![]() or
or
![]() are abbreviations for
are abbreviations for
![]() : this means that
: this means that ![]() is expressed as a function of
is expressed as a function of ![]() .
For instance, the sequence (1) above can be described by
the explicit formula
.
For instance, the sequence (1) above can be described by
the explicit formula
![]() .
.