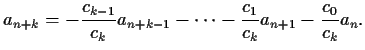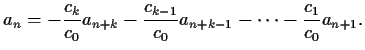Next: Characteristic polynomials
Up: Linear recursive sequences
Previous: Recursive definitions
Linear recursive sequences
A sequence 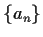 is said to satisfy the linear recurrence
with coefficients
is said to satisfy the linear recurrence
with coefficients 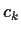 ,
, 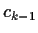 , ...,
, ..., 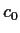 if
if
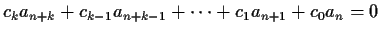 |
(2) |
holds for all integers 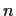 for which this makes sense.
(If the sequence starts with
for which this makes sense.
(If the sequence starts with 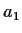 , then this means for
, then this means for 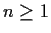 .)
The integer
.)
The integer 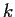 is called the order of the linear recurrence.
is called the order of the linear recurrence.
A linear recursive sequence
is a sequence of numbers
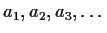 satisfying some linear recurrence as above
with
satisfying some linear recurrence as above
with
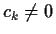 and
and
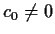 .
For example, the sequence (1) satisfies
.
For example, the sequence (1) satisfies
for all integers 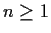 ,
so it is a linear recursive sequence satisfying
a recurrence of order 1,
with
,
so it is a linear recursive sequence satisfying
a recurrence of order 1,
with 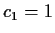 and
and 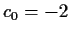 .
.
Requiring
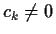 guarantees that
the linear recurrence can be used to express
guarantees that
the linear recurrence can be used to express 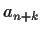 as a linear combination of earlier terms:
as a linear combination of earlier terms:
The requirement
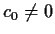 lets one express
lets one express 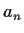 as a linear combination of later terms:
This lets one define
as a linear combination of later terms:
This lets one define 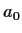 ,
, 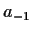 , and so on,
to obtain a doubly infinite sequence
that now satisfies the same linear recurrence for all integers
, and so on,
to obtain a doubly infinite sequence
that now satisfies the same linear recurrence for all integers 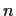 ,
positive or negative.
,
positive or negative.



Next: Characteristic polynomials
Up: Linear recursive sequences
Previous: Recursive definitions
Zvezdelina Stankova-Frenkel
2000-09-20
![]() is said to satisfy the linear recurrence
with coefficients
is said to satisfy the linear recurrence
with coefficients ![]() ,
, ![]() , ...,
, ..., ![]() if
if
![]() satisfying some linear recurrence as above
with
satisfying some linear recurrence as above
with
![]() and
and
![]() .
For example, the sequence (1) satisfies
.
For example, the sequence (1) satisfies
![]() guarantees that
the linear recurrence can be used to express
guarantees that
the linear recurrence can be used to express ![]() as a linear combination of earlier terms:
as a linear combination of earlier terms: