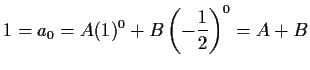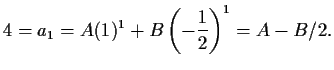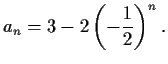Next: Example: the formula for
Up: Linear recursive sequences
Previous: The main theorem
Suppose we want to find an explicit formula for
the sequence 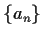 satisfying
satisfying 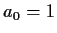 ,
, 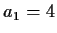 ,
and
,
and
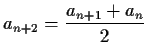 for for 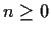 . . |
(6) |
Since 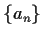 satisfies a linear recurrence with characteristic polynomial
satisfies a linear recurrence with characteristic polynomial
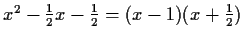 ,
we know that there exist constants
,
we know that there exist constants  and
and  such that
such that
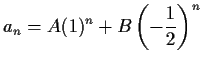 |
(7) |
for all 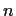 .
The formula (7) is called the general solution
to the linear recurrence (6).
To find the particular solution with the correct values of
.
The formula (7) is called the general solution
to the linear recurrence (6).
To find the particular solution with the correct values of 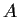 and
and 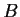 ,
we use the known values of
,
we use the known values of 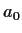 and
and 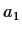 :
Solving this system of equations yields
:
Solving this system of equations yields 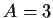 and
and 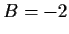 .
Thus the particular solution is
(As a check, one can try plugging in
.
Thus the particular solution is
(As a check, one can try plugging in 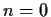 or
or 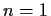 .)
.)
Zvezdelina Stankova-Frenkel
2000-09-20
![]() satisfying
satisfying ![]() ,
, ![]() ,
and
,
and