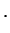The main theorem

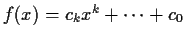
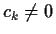
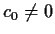
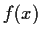
Theorem 1   Let $f(x)=c_k x^k + \cdots + c_0$ be a polynomial with $c_k \not= 0$ and $c_0 \not=0$. Factor $f(x)$ over the complex numbers as

$$f(x) = c_k (x-r_1)^{m_1} (x-r_2)^{m_2} \cdots (x-r_\ell)^{m_\ell},$$

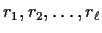
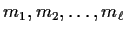
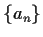
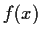
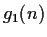
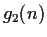
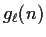
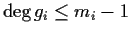
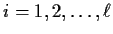
where $r_1,r_2,\dots,r_\ell$ are distinct nonzero complex numbers, and $m_1,m_2,\dots,m_\ell$ are positive integers. Then a sequence $\{a_n\}$ satisfies the linear recurrence with characteristic polynomial $f(x)$ if and only if there exist polynomials $g_1(n)$, $g_2(n)$, ..., $g_\ell(n)$ with $\deg g_i \le m_i-1$ for $i=1,2,\dots,\ell$ such that

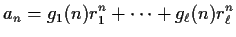
$$a_n = g_1(n) r_1^n + \cdots + g_\ell(n) r_\ell^n$$   for all $n$$$.$$

Here is an important special case.

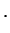
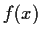
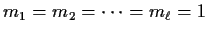
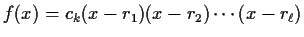
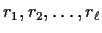
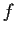
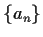
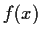
Corollary 2   Suppose in addition that $f(x)$ has no repeated factors; in other words suppose that $m_1=m_2=\cdots=m_\ell=1$. Then $f(x)=c_k(x-r_1)(x-r_2)\cdots(x-r_\ell)$ where $r_1,r_2,\dots,r_\ell$ are distinct nonzero complex numbers (the roots of $f$). 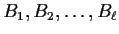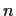Then $\{a_n\}$ satisfies the linear recurrence with characteristic polynomial $f(x)$ if and only if there exist constants $B_1, B_2, \dots, B_\ell$ (not depending on $n$) such that

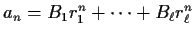
$$a_n = B_1 r_1^n + \cdots + B_\ell r_\ell^n$$   for all $n$$$.$$