


Next: Bezout's Theorem
Up: Algebraic Geometry
Previous: Examples of Varieties
Definitions.
- (a)
- An ideal
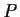 of a ring
of a ring 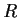 is called prime if whenever
is called prime if whenever
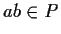 for
for 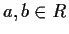 , then
, then 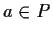 or
or 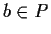 (or both).
(or both).
- (b)
- A variety
 is called irreducible if for any
decomposition
is called irreducible if for any
decomposition
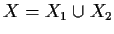 of
of  into a union of two subvarieties,
either
into a union of two subvarieties,
either 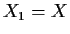 or
or 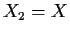 . In other words, there are no non-trivial
decompositions of
. In other words, there are no non-trivial
decompositions of  into smaller varieties.
into smaller varieties.
Proposition 2
A variety

is irreducible iff its ideal
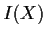
is prime.
Thus, there exists a one-to-one correspondence between the set of
varieties
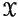 and the set of prime (homogeneous if
projective
and the set of prime (homogeneous if
projective  ) ideals
) ideals
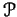 in the corresponding polynomial
ring.
in the corresponding polynomial
ring.
Theorem 4
Any radical ideal
![$ I\subset
K[x_1,...,x_n]$](img12.gif)
is uniquely
expressible as a finite intersection of prime ideals
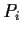
with
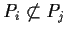
for
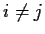
. Equivalently, any
variety

can be uniquely expressed as a finite union of irreducible
subvarieties
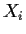
with
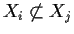
for
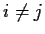
.
The varieties 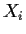 appearing in this unique decomposition
are called the irreducible components of
appearing in this unique decomposition
are called the irreducible components of  .
.
Definition. Let  be a set of points in some
space. A topology on
be a set of points in some
space. A topology on  is a set
is a set
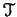 of designated
subsets of
of designated
subsets of  , called the open sets of
, called the open sets of  , so that the
following axioms are satisfied:
, so that the
following axioms are satisfied:
- (a)
- The union of any collection of open sets is open.
- (b)
- The intersection of any finite collection of open sets
is open.
- (c)
 and
and 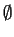 are open.
are open.
The closed sets in  are the complements of the
open sets.
are the complements of the
open sets.
We define below the so-called Zariski topology on
algebraic varieties. If we work over
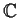 , every variety can
be roughly viewed as a complex manifold
, every variety can
be roughly viewed as a complex manifold  (with the exception
of a proper subset of its singular points). Through its
embedding in, say,
(with the exception
of a proper subset of its singular points). Through its
embedding in, say,
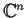 ,
,  will inherit the usual complex analytic topology from
will inherit the usual complex analytic topology from
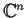 - a basis for the open
sets on
- a basis for the open
sets on  will consist of the intersections of
will consist of the intersections of  with any finite
balls in
with any finite
balls in
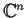 .
.
The Zariski topology is a different kind of topology. A basis
for the open sets in  is given by the sets
where
is given by the sets
where 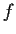 ranges over polynomials (homogeneous if projective
ranges over polynomials (homogeneous if projective  ).
).
Lemma 2
The Zariski topology is indeed a topology on

.
Exercise. Show that the Zariski topology on the
projective line
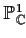 is different from the
analytic topology of
is different from the
analytic topology of
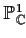 .
.
Many statements in algebraic geometry are true for general points on varieties, i.e. if  is a variety and
is a variety and 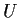 is an
open dense set of
is an
open dense set of  , then any point
, then any point 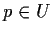 is called a general point on
is called a general point on 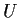 . (If
. (If  is irreducible, then any nonempty open
set will be dense. This, in particular, makes Zariski topology a non-Housdorff topology - in the latter, one needs for any two points
of
is irreducible, then any nonempty open
set will be dense. This, in particular, makes Zariski topology a non-Housdorff topology - in the latter, one needs for any two points
of  to have two nonintersecting open sets containing each one of
the points. This confirms once again that the Zariski topology is
much coarser than the analytic topology.)
to have two nonintersecting open sets containing each one of
the points. This confirms once again that the Zariski topology is
much coarser than the analytic topology.)



Next: Bezout's Theorem
Up: Algebraic Geometry
Previous: Examples of Varieties
Zvezdelina Stankova-Frenkel
2001-01-24
![]() and the set of prime (homogeneous if
projective
and the set of prime (homogeneous if
projective ![]() ) ideals
) ideals
![]() in the corresponding polynomial
ring.
in the corresponding polynomial
ring.
![]() appearing in this unique decomposition
are called the irreducible components of
appearing in this unique decomposition
are called the irreducible components of ![]() .
.
![]() be a set of points in some
space. A topology on
be a set of points in some
space. A topology on ![]() is a set
is a set
![]() of designated
subsets of
of designated
subsets of ![]() , called the open sets of
, called the open sets of ![]() , so that the
following axioms are satisfied:
, so that the
following axioms are satisfied:
![]() are the complements of the
open sets.
are the complements of the
open sets.
![]() , every variety can
be roughly viewed as a complex manifold
, every variety can
be roughly viewed as a complex manifold ![]() (with the exception
of a proper subset of its singular points). Through its
embedding in, say,
(with the exception
of a proper subset of its singular points). Through its
embedding in, say,
![]() ,
, ![]() will inherit the usual complex analytic topology from
will inherit the usual complex analytic topology from
![]() - a basis for the open
sets on
- a basis for the open
sets on ![]() will consist of the intersections of
will consist of the intersections of ![]() with any finite
balls in
with any finite
balls in
![]() .
.
![]() is different from the
analytic topology of
is different from the
analytic topology of
![]() .
.