


Next: About this document ...
Up: Algebraic Geometry
Previous: Zariski Topology
Definition. Suppose that  and
and
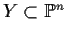 are
two irreducible varieties and that their intersection has irreducible
components
are
two irreducible varieties and that their intersection has irreducible
components 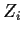 . We say that
. We say that  and
and 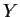 intersect generically
transversally if, for each
intersect generically
transversally if, for each 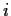 ,
,  and
and 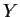 intersect transversally at
a general point
intersect transversally at
a general point
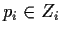 , i.e., are smooth at
, i.e., are smooth at 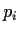 with tangent spaces spanning
with tangent spaces spanning
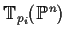 (the tangent space to
(the tangent space to
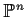 at
at 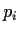 .)
.)
Theorem 5 (Bezout)
Let

and
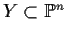
be
subvarieties of pure dimensions
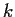
and
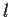
with
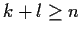
, and
suppose they intersect generically transversely. Then
In particular, if
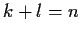
, this says that
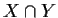
will consist of
deg
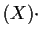
deg
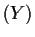
points.
A pair of pure-dimensional varieties  and
and
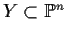 intersect properly if their intersection has the expected
dimension, i.e.,
intersect properly if their intersection has the expected
dimension, i.e.,
Theorem 6
If

and
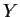
intersect properly,
where the sum is over
all irreducible subvarieties
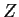
of the appropriate dimension (in
effect, over all irreducible components
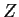
of
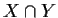
). Here
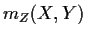
is the
intersection multiplicity of

and
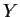
along
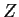
:
- 1.
-
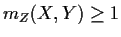 for all
for all
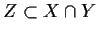 (
(
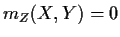 otherwise.)
otherwise.)
- 2.
-
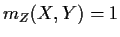 if
if  and
and 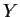 intersect transversely at a general
point of
intersect transversely at a general
point of 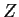 .
.
- 3.
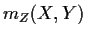 is additive, i.e.
is additive, i.e.
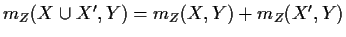 for any
for any  and
and
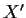 as long as
all three numbers are defined and
as long as
all three numbers are defined and  and
and
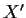 have no common
components.
have no common
components.
In particular, for any subvarieties  and
and 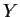 of
pure dimension in
of
pure dimension in
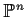 intersecting properly:
intersecting properly:



Next: About this document ...
Up: Algebraic Geometry
Previous: Zariski Topology
Zvezdelina Stankova-Frenkel
2001-01-24
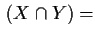 deg
deg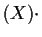 deg
deg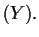
![]() and
and
![]() intersect properly if their intersection has the expected
dimension, i.e.,
intersect properly if their intersection has the expected
dimension, i.e.,
![]() and
and ![]() of
pure dimension in
of
pure dimension in
![]() intersecting properly:
intersecting properly: