Examples of Varieties

Example 1. Let $Q$ be the (smooth) quadric surface in $\mathbb{P}^3$ given as the zero locus of one homogeneous quadratic equation:

$$Q=Z(Z_0Z_3-Z_1Z_2).$$

The quadric $Q$ consists of two families of lines, each of which sweeps $Q$ on its own:

$$\{Z_1=\lambda Z_0,\,\,Z_3=\lambda Z_2\}\,\,$$and$$\,\,\{Z_2=\mu Z_0,\,\,Z_3=\mu Z_1\}.$$

In terms of the matrix

$$M=\left(\begin{array}{ll} Z_0& Z_1\\ Z_2& Z_3 \end{array}\right),$$

$Q$ is the locus where det$M=0$, one family of lines consists of lines where the two column satisfy a given linear relation, the other family - where the two rows satisfy a given linear relation. Note that two lines in a family do not intersect (they are skew lines in $\mathbb{P}^3$), while any two lines from different families intersect in exactly one point. The latter hints at an alternative description of $Q$ - namely as the ``Cartesian product'' $\mathbb{P}^1\times \mathbb{P}^1$.

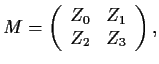
More generally, for any two varieties $X$ and $Y$, there is a (unique) variety $X\times Y$ with projection maps $\pi_1:X\times Y\rightarrow X$ and $\pi_2:X\times Y\rightarrow Y$, the fibers of which are correspondingly copies of $Y$ and of $X$. The uniqueness of such a variety is ensured by some extra (natural) properties coming from category theory - such properties are exactly what we would expect from a variety deserving to be called the ``product'' of two varieties.

The actual construction of this product is given by a (seemingly random) map, called the Segre embedding. For starters, to construct the product $\mathbb{P}^n\times \mathbb{P}^m$, we define the Segre map by

$$\sigma_{n,m}:\mathbb{P}^n_{[X]}\times \mathbb{P}^m_{[Y]}\rightarrow \mathbb{P}^{(n+1)(m+1)-1}_{[Z]}$$

$$\sigma_{n,m}([X_0,...,X_n],[Y_0,...,Y_m])=[X_0Y_0,...,X_iY_j,...,X_nY_m].$$

If we label the coordinates on $\mathbb{P}^{(n+1)(m+1)-1}_{[Z]}=\mathbb{P}^N$ by $Z_{ij}$ for $0\leq i\leq n$ and $0\leq j\leq m$, then the image of $\sigma_{n,m}$ is the zero locus of all possible quadratic equations $Z_{ij}Z_{kl}=Z_{il}Z_{kj}$. Thus, the image of the Segre map is a variety. Factoring into this the injectivity of $\sigma_{n,m}$, allows us to ``identify'' the set-product $\mathbb{P}^n\times \mathbb{P}^m$ with a subvariety of $\mathbb{P}^N$, which is define as the product of $\mathbb{P}^n$ and $\mathbb{P}^m$ in the category of varieties. One can show that this particular variety satisfies all the required properties of a product, and by virtue of the uniqueness of the product, it is The product variety $\mathbb{P}^n\times \mathbb{P}^m$.

Now it is not hard to construct the product of any two varieties $X$ and $Y$: if $X\subset \mathbb{P}^n$ and $Y\subset \mathbb{P}^m$, then $X\times Y$ is the subvariety of $\mathbb{P}^n\times \mathbb{P}^m$, satisfying the extra equations coming from $X$ and $Y$.

Example 2. The twisted cubic curve $C$ is the zero locus of three polynomials:

$$C=Z(Z_0Z_3-Z_1Z_2, Z_0Z_2-Z_1^2, Z_1Z_3-Z_2^2).$$

The twisted cubic $C$ lies on the quadric surface $Q$, and is a curve of type $(2,1)$ on $Q$, i.e. $C$ meets every line in one family in 2 points, and every line in the other family - in 1 point (prove this!) Prove also that the zero locus of any two of the three quadratic polynomials defining $C$ is the union of $C$ and a line on $Q$ meeting $C$ in two points (or being tangent to $C$). How many such tangent lines to $C$ are there in the family consisting generically of lines meeting $C$ in two points?

An alternative description of $C$ is the image of the Veronese embedding of $\mathbb{P}^1$ in $\mathbb{P}^3$:

$$C=\{[X^3,X^2Y,XY^2,Y^3]\,\,\vert\,\,[X,Y]\in\mathbb{P}^1\}=\nu_3(\mathbb{P}^1).$$

Show that this is indeed an embedding, and that its image indeed coincides with the twisted cubic curve $C$.

Example 3. What are the hyperplane sections of $Q$, i.e. $\mathbb{P}^2\cap Q$, as the hyperplane $\mathbb{P}^2$ varies in $\mathbb{P}^3$?

The strategy here is to restrict the equation of $Q$ to the hyperplane $\mathbb{P}^2$, and to realize that a homogeneous quadratic polynomial in 3 variables is either irreducible (smooth plane conic hyperplane section of $Q$), or factors as the product of two homogeneous linear factors (the hyperplane section here is the union of two intersecting lines in $\mathbb{P}^2$). Prove that we will never get the quadratic polynomial to factor as a perfect square of a linear form (i.e. no hyperplane in $\mathbb{P}^3$ intesects $Q$ in a ``double line'').

We push the above considerations an inch further to ask the following question: can we construct a variety $\mathcal{H}_{Q}$ which in some reasonable way will be the family of all hyperplane sections of $Q$? In other words, can we separate all hyperplane sections of $Q$, so that they do not intersect anymore, but stay as fibers of some map? The answer is ``YES'', yet we have to work a bit to construct this variety.

For starters, we can construct the universal hyperplane $\mathcal{H}$ in $\mathbb{P}^3$ - apriori, we want this to be a variety, representing all hyperplanes in $\mathbb{P}^3$, in other words, $\mathcal{H}$ should be a family of all hyperplanes in $\mathbb{P}^3$. The first step is to realize what variety parametrizes these hyperplanes - this is the dual $(\mathbb{P}^3)^*$, which is really $\mathbb{P}^3$ all over again, by with different coordinates. If $\mathbb{P}^3$ has coordinates $[Z_0,Z_1,Z_2,Z_3]$, then a hyperplane in $\mathbb{P}^3$ is given by a linear form $W_0Z_0+W_1Z_1+W_2Z_2+W_3Z_3=0$ for some fixed $[W_0,W_1,W_2,W_3]\in (\mathbb{P}^3)^*$. Thus, the dual $(\mathbb{P}^3)^*$ has coordinates $W_0,W_1,W_2,W_3$; points in $(\mathbb{P}^3)^*$ correspond to hyperplanes in $\mathbb{P}^3$, and hyperlanes in $(\mathbb{P}^3)^*$ correspond to points in $\mathbb{P}^3$.

Now, the universal hyperplane $\mathcal{H}$ should be defined as a set by

$$\mathcal{H}=\{[p,H]\,\,\vert\,\,p\in\mathbb{P}^3,\,\,H\in (\mathbb{P}^3)^*, \,\,p\in H\}.$$

Therefore, we naturally consider $\mathcal{H}\in \mathbb{P}^3\times (\mathbb{P}^3)^*$ - it is the zero locus of a single bihomogeneous polynomial:

$$W_0Z_0+W_1Z_1+W_2Z_2+W_3Z_3=0.$$

In terms of the coordinates $T_{ij}$ on $\mathbb{P}^{15}$, in which $\mathbb{P}^3\times (\mathbb{P}^3)^*$ is embedded, this polynomial reads:

$$T_{00}+T_{11}+T_{22}+T_{33}=0.$$

We conclude that $\mathcal{H}$ is a subvariety of the product $\mathbb{P}^3\times (\mathbb{P}^3)^*$; more precisely, it is a hyperplane section of $\mathcal{H}$ inside $\mathbb{P}^{15}$.

Finally, to construct the universal hyperplane section $\mathcal{H}_Q$ of the quadric $Q$, we only have to intersect with $\mathcal{H}$:

$$\mathcal{H}_Q=Q\cap \mathcal{H}\subset \mathbb{P}^3\times (\mathbb{P}^3)^*.$$

Since the product on the right has two natural projections $\pi_1$ and $\pi_2$ onto the two factors $\mathbb{P}^3$ and $(\mathbb{P}^3)^*$, we can restrict these maps to $\mathcal{H}_Q$, and ask what the fibers of $\pi_1$ - $\pi_2$ are. Prove that the fibers of $\pi_1$ are all (isomorphic to) $\mathbb{P}^3$, while the fibers of $\pi_2$ are the hyperplane sections of $Q$ - what we wanted in the first place.

Maps of varieties $\phi:X\rightarrow Y$ whose fibers are all isomorphic to some $\mathbb{P}^k$ are called $\mathbb{P}^k$- bundles over $Y$. Sometimes it is important to classify all such bundles over a fixed variety $Y$ - this describes additional invariants of $Y$, which may be used for instance to identify two non-isomorphic varieties.

Example 4. As we saw above, all hyperplanes in $\mathbb{P}^3$ can be parametrized by the variety $(\mathbb{P}^3)^*$ (which is isomorphic to $\mathbb{P}^3$.) In this case, the points of $(\mathbb{P}^3)^*$ are in 1-1 correspondence with the hyperplanes in question, and $(\mathbb{P}^3)^*$ reflects (in a certain sense) how the hyperplanes vary in $\mathbb{P}^3$ - that is, for any ``nice'' family $\mathcal{F}$ of hyperplanes in $\mathbb{P}^3$ the subset of $(\mathbb{P}^3)^*$ corresponding to $\mathcal{F}$ is a subvariety of $(\mathbb{P}^3)^*$. (The word ``nice'' has a very technical meaning, usually called ``flatness'' of families. We shall not discuss this here since it will take us too far afield.)

One can easily generalize the above construction to parametrize all hyperplanes in $\mathbb{P}^n$ by the dual projective space $(\mathbb{P}^n)^*$. A natural question arises: Can we find varieties parametrizing other objects, say, conics in $\mathbb{P}^2$? Such varieties are called parameter spaces.

Let $\mathcal{P}$ be the set of all conics in $\mathbb{P}^2$. If we fix the coordinates of $\mathbb{P}^2$ to be $X,Y,Z$, then a conic $C$ is determined upto a scalar by a quadratic equation:

$$a_0X^2+a_1Y^2+a_2Z^2+a_3XY+a_4YZ+a_5ZX=0.$$

Such an equation determines a projective point $[a_0,a_1,...,a_5]\in \mathbb{P}^5$, and conversely, any point of $\mathbb{P}^5$ determines a unique quadratic polynomial (upto a scalar). Thus, the parameter space for all conics in $\mathbb{P}^2$ is $\mathcal{P}=\mathbb{P}^5$.

Similarly, the parameter space of all hypersurfaces of degree $d$ in $\mathbb{P}^n$ (i.e. subvarieties given by single degree $d$ homogeneous polynomials on $\mathbb{P}^n$) is $\mathcal{P}_{d,n}=\mathbb{P}^{N}$ where $N=\binom{n+d}{d}-1$. Note a slight technicality here: we have included as points in $\mathcal{P}_{d,n}$ ``hypersurfaces'' corresponding to polynomials with multiple factors. For example, in the case of conics in $\mathbb{P}^2$, we included as points in $\mathcal{P}_{2,2}$ all ``double'' lines. One can show that the set of such ``multiple'' (or more precisely, non-reduced) hypersurfaces is in fact a subvariety of the corresponding parameter space $\mathcal{P}_{d,n}$.

Example 5. Parameter spaces parametrize usually not just objects $X$ sharing some common properties, but also the embeddings of $X$ in projective space. For example, there are really only three types of conics in $\mathbb{P}^2$ - the irreducible (smooth) conics, the joins of two different lines, and the double lines. Every irreducible conic can be transformed into any other irreducible conic after a suitable change of variables (coordinate change) on $\mathbb{P}^2$, etc. Thus, in constructing $\mathcal{P}_{2,2}$, we grossly ``overcounted'' the irreducible conics (well, we were parametrizing, therefore, not just the conics, but the pairs $(C,\phi)$ where $C$ is a plane conic and $\phi:C\hookrightarrow \mathbb{P}^2$ is an embedding.)

The philosophy of viewing a variety as an object with a given embedding in some $\mathbb{P}^n$ is inherent to XIX century algebraic geometry, especially to the Italian school. XX century changed this view by considering varieties as objects on their own, disregarding particular embeddings in projective space. For example, any irreducible conic in $\mathbb{P}^2$ is really a $\mathbb{P}^1$ embedded in a certain way in $\mathbb{P}^2$:

$$\nu_2:\mathbb{P}^1\hookrightarrow \mathbb{P}^2,\,\, \nu_2([X,Y])=[X^2,XY,Y^2].$$

Similarly, the twisted cubic $C$ in $\mathbb{P}^3$ is isomorphic to $\mathbb{P}^1$: $C=\nu_3(\mathbb{P}^3)$. We say that these curves are isomorphic to each other because there exist nicely defined maps via polynomials going back and forth between these varieties, whose compositions are identities. Thus, the intrinsic properties of $\mathbb{P}^1$ are preserved under these isomorphism, and therefore the embeddings do not change the actual variety.

Some extrinsic properties, however, change, and these cause the different embeddings of $\mathbb{P}^1$ to look different. For example, define the degree of $X\cong\mathbb{P}^1\subset \mathbb{P}^n$ to be the number of points in the intersection of a general hyperplane in $\mathbb{P}^n$ with $X$. Thus, the conics in $\mathbb{P}^2$ have degree $2$, and will keep their degree if we embed now $\mathbb{P}^2$ as a linear subspace of a bigger $\mathbb{P}^n$. However, the twisted cubic $C$ in $\mathbb{P}^3$ has degree $3$ (one way to see this is to recall that a line in one ruling meets $C$ in 1 point, while a line in the other ruling meets $C$ in 2 points.)

While parameter spaces may take into account such extrinsic properties as degrees of varieties, moduli spaces usually parametrize objects according to only their intrinsic properties, and hence are much harder to be constructed. To even state what common instrinsic properties can be characterized will take too much ink on this handout. But let us mention one very famous example - the moduli space $\mathfrak{M}_g$ of smooth curves of genus $g$. ¹ These curves do not lie (and cannot be embedded in general) in the same projective space $\mathbb{P}^n$. The best we can say is that each such (non-hyperelliptic) curve can be embedded in $\mathbb{P}^{2g-3}$, but we don't care about these embeddings anyways. Yet, $\mathfrak{M}_g$ can be constructed, and it is a variety of dimension $3g-3$ for $g\geq 2$. For $g=1$ there is only one such curve - $\mathbb{P}^1$, so $\mathfrak{M}_1$ is really just one point; for $g=1$ - the elliptic curves can be effectively parametrized by a certain cross ratio, and hence $\mathfrak{M}_1\cong \mathbb{P}^1$.

A further development of this theory is the Deligne-Mumford compactification of $\mathfrak{M_g}$. Since $\mathfrak{M}_g$ is not a projective variety, one can have a nice family of smooth curves degenerating to a singular curve, but $\mathfrak{M}_g$ does not have any points to reflect the limiting singular member of the family. The question arises - what is the ``minimal'' set of singular curves must be added to the set of smooth curves in order to obtain a ``nice'' moduli space $\overline{\mathfrak{M}}_g$, compactifying $\mathfrak{M}_g$? Deligne and Mumford chose (and for very good reasons) the set of the so-called stable curves $C$ of genus $g$. These are connected curves with at most nodal type of singularities (e.g. take two lines intersecting in $\mathbb{P}^2$), and such that if they contain a $\mathbb{P}^1$-component, then the latter must meet at least 3 other components of the curve. The last condition is added to ensure that the curves have finite groups of automorphisms. With this said, $\overline{\mathfrak{M}}_g$ is the moduli space of all stable curves of genus $g$. It is a projective variety which contains $\mathfrak{M}_g$ as an open dense set, and it reflects naturally the variation of ``nice'' families of stable curves. Moreover, any ``nice'' family whose general members are smooth curves, but whose special members can be as nasty as you wish, can be brought in an essentially one way to a family with only stable members. This process is called semistable reduction and it is the basis for many related constructions in algebraic geometry.