Varieties, Ideals, Nullstellensatz

Let $K$ be a field. We shall work over $K$, meaning, our coefficients of polynomials and other scalars will lie in $K$.

Definitions.

1.

An affine variety $X$ in $\mathbb{A}^n$ is the zero locus of a collection of polynomials $\{f(x_1,...,x_n)\}$ in $K[x_1,...,x_n]$. A projective variety X in $\mathbb{P}^n$ is the zero locus of a collection of homogeneous polynomials $\{F(Z_0,...,Z_n)\}$ in $K[Z_0,...,Z_n]$.

2.

For a given variety $X$, the set of all polynomials vanishing on $X$ is an ideal, called the ideal of $X$ and denoted by $I(X)$. In other words,

$$I(X)=(...,f_{\alpha},...)\,\,$$or$$\,\,I(X)=(...,F_{\alpha},...),$$

depending on whether the variety is affine or projective. In the second case, the ideal is called homogeneous, i.e. generated by homogeneous polynomials. Conversely, for a given ideal $I\subset K[x_1,...,x_n]$ (or homogeneous $I\subset K[Z_0,...,Z_n]$), the zero locus of $I$ is denoted by $Z(I)$.

Projective varieties can be thought of as ``completions'', ``compactifications'', or ``closures'' of affine varieties. Their global properties are usually easier to describe than those of affine varieties. Conversely, affine varieties can be thought of as building blocks of projective varieties (indeed, they constitute an open cover), and hence local properties are easier to describe using affine varieties. However, projective varieties vary ``nicely'' in families and hence parametrizing and moduli spaces are usually constructed for projective varieties with certain defining common properties.

3.

A ring $R$ is called Noetherian if any inscreasing sequence of ideals terminates, i.e. whenever $I_j$'s are ideals in $R$ such that

$$I_1\subset I_2\subset \cdots \subset I_j \subset \cdots$$

then for some $k\geq 1$: $I_k=I_{k+1}=I_{k+2}=\cdots$

4.

An ideal $I$ in a ring $R$ is called radical if whenever $f^m\in I$ ($f\in R$, $m\in\mathbb{N}$), then $f\in I$. In other words, $I$ contains all (positive integer) roots of its elements.

Theorem 1   The polynomial ring $R=K[x_1,x_2,...,x_n]$ is Noetherian. Consequently, any ideal $I$ of $R$ is finitely generated. In particular, for any affine (or projective) variety $X$, the ideal $I$ of $X$ is generated by finitely many polynomials.

Lemma 1   The ideal of any algebraic variety $X$ is radical. If $I$ is an arbitrary ideal, the set of all radicals of its elements:

$$\sqrt{I}:=\{f\in R\,\,\vert\,\,f^n\in I\,\,$$for some$$\,\,n\in\mathbb{N}\}$$

is also an ideal, called the radical of $I$. If $I$ is a radical ideal, then its radical is itself, i.e. the operation of taking radicals stabilizes after one step.

We construct maps bewteen the set $\mathcal{X}$ of all varieties $X$ over $K$ and the set $\mathcal{J}$ of all ideals $J\subset K[x_1,...,x_n]$ by sending

$$i:X\mapsto I(X)\,\,\,$$   and$$\,\,\,j:J\mapsto Z(J).$$

It is immediate from definition of an ideal of variety that $Z(I(X))=X$, i.e. $j\circ i=$id$_{\mathcal X}$. Also, the image of $i$ is inside $\mathcal{R}$, the subset of radical ideals in $R$. Thus, we have an injection $i:\mathcal{X}\hookrightarrow \mathcal{R}$ with a one-way inverse $j:\mathcal{R}\rightarrow \mathcal{X}$. It is natural to ask whether $i$ and $j$ are inverses of each other, i.e. whether $i\circ j=$id$_{\mathcal R}$.

For any ideal $J\subset \mathcal{J}$ (not necessarily radical), we consider $X:=Z(J)=j(J)$ - a variety, and then take $i(X)=I(X)=I(Z(J))$. It is evident that $I(X)$ will be a radical ideal containing $J$, but is it going to be $\sqrt{J}$? To paraphrase the problem, start with $J$ being a radical ideal and take $I(Z(J))$. Is this equal to $J$?

The answer in general is no. For example, if $K=\mathbb{R}$ is the ground field, and $J=(x^2+y^2)$ is the ideal generated by the single polynomial $f(x,y)=x^2+y^2$ in the affine plane, then $J$ is obviously radical ($f$ is irreducible), and the zero locus of $J$ is $Z(J)=(0,0)$ - just one point. However, the ideal of $(0,0)$ is definitely much larger than $J$ - it consists of all polynomials vanishing at $(0,0)$, i.e. having no free terms: $I((0,0))=(x,y)\supset (x^2+y^2)$. Thus, we end up with a (radical) ideal bigger than the original.

The above situation is possible because $\mathbb{R}$ is not an algebraically closed field. This leads to the famous Nullstelensatz, a basic theorem in commutative algebra, on which much of algebraic geometry over algebraically closed fields is based.

Theorem 2 (Nullstelensatz)   If $K$ is an algebraically closed field, then for any ideal $J\subset K[x_1,...,x_n]$:

$$i\circ j(J)= I(Z(J))=\sqrt{J}.$$

In particular, there is a one-to-one correspondence between the set $\mathcal{X}$ of affine varieties $X$ in $\mathbb{A}^n$ and radical ideals $\mathcal{R}$ given by

$$i:\mathcal{X}\rightarrow \mathcal{R},\,\,$$and$$\,\,j:\mathcal{R} \rightarrow \mathcal{X}.$$

Note that the radical of the unit ideal is again the unit ideal: $\sqrt{(1)}=(1)$. This implies the following corollary:

Corollary 1   If $f_1,...,f_k$ are polynomials in several variables over an algebraically closed field $K$, then they have no common zeros in $K$ iff

$$1=g_1f_1+g_2f_2+\cdots+g_kf_k$$

for some polynomials $g_1,g_2,...,g_k$.

Some other ``strange'' things happen over fields, which are not algebraically closed. For example, we would like to call a ``planar curve'' any variety $X$ in $\mathbb{A}^2$ which is given by 1 polynomial. However, over $\mathbb{R}$, the ``curve'' defined by $x^2+y^2=0$ is really just a point, while over $\mathbb{C}$ (or any algebraically closed fields) it is a pair of intersecting lines. Thus, many interesting and intuitive properties of algebraic varieties hold only over algebraically closed fields.

There is an analog of Nullstelensatz for projective varieties (for $K=\overline{K}$, of course.) There is one subtle point, though. We call $Ir=(Z_0,...,Z_n)$ the irrelevant ideal in $K[Z_0,Z_1,...,Z_n]$. Note that $Ir$ is radical, and that $Z(Ir)=\emptyset$. Yet, $Ir$ is not the whole ideal of $\emptyset$: $(1)=K[Z_0,Z_1,...,Z_n]$, the unit ideal, is the ideal of $\emptyset$. Thus, we have two radical ideals competing for the $\emptyset$: $Z(Ir)=Z((1))=\emptyset$. The bigger one ``wins'', because $I(\emptyset)=(1)$, and we state the Nullstelensatz as follows:

Theorem 3   There is a one-to-one correspondence between the set $\mathcal{X}$ of projective varieties $X\subset \mathbb{P}^n$ and the set $\mathcal{R}$ of radical homogeneous ideals minus $Ir$ given by $i$ and $j$ from above. In particular, for $J\in\mathcal{J}$:

$$I(Z(J))=\left\{\begin{array}{ll} \sqrt{J} & \text{if}\,\,Z(J)\not = \emptyset\\ (1) & \text{if}\,\,Z(J)=\emptyset. \end{array}\right.$$

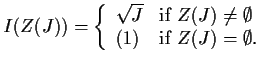
Note further that for a (homogeneous) ideal $J$, $Z(J)=\emptyset$ iff $\sqrt{J}=(1)$ or $\sqrt{J}=(Z_0,Z_1,...,Z_n)$. In both cases, $\sqrt{J}\supset (Z_0,Z_1,...,Z_n)$, which can be shown to imply $J\supset (Z_0,Z_1,...,Z_n)^d$ for some $d>0$.

Proposition 1   Let $J$ be a homogeneous ideal. Then $Z(J)=\emptyset$ iff $J$ contains a power of the irrelevant ideal. In other words, a collection of homogeneous polynomials $\{F_{\alpha}\}$ will have no common zeros iff the ideal generated by the $F_{\alpha}$'s contains all (homogeneous) polynomials of a certain degree $d>0$.