


Next: Three Impossible Constructions
Up: Algebraic Equivalent
Previous: Arithmetic Exercises
Now imagine that the given points and the required points are drawn in
some nice Cartesian coordinate system. Then finding new points is
equivalent to finding their coordiantes. In other words, a construction
problem can be restated in an algebraic form something like this:
- Given a set of pairs of coordinates:
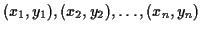 , construct other pairs of coordinates
, construct other pairs of coordinates
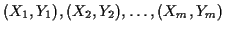 using the following algebraic transformations ....
using the following algebraic transformations ....
As we'll see below, those ``algebraic transformations'' are pretty simple
to describe, and such a description will allow us to identify the sorts of
sets of coordinates that can be constructed using a straightedge and
compass.
Here's the idea--we just need to know how to how each of the allowed
geometric constructions translates into algebra. Let's take a look:
- You can draw a line through two points. Well, it is
easy to write down the equation of a line passing through
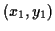 and
and
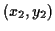 :
:
- You can draw a circle with any point as center and
any other point on the boundary. If
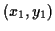 is the center,
and
is the center,
and 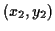 is a point on the boundary, we know the radius
is a point on the boundary, we know the radius 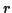 is
given by:
is
given by:
Then the equation
of a circle centered at 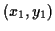 and having radius
and having radius 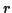 is given by:
is given by:
- You can find the intersection of any two lines. Again,
this is easy--if the given lines have the equations
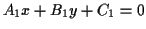 and
and
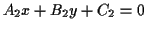 , a simultaneous solution of these two equations
is simply a matter of algebra, and the result is just an equation in the
variables
, a simultaneous solution of these two equations
is simply a matter of algebra, and the result is just an equation in the
variables
 and
and 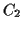 .
.
- You can find points that are the intersection of a line
and a circle. In this case, suppose the line has equation
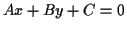 ,
and that the circle has equation
,
and that the circle has equation
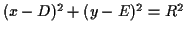 . Then we
can solve the equation of the line for
. Then we
can solve the equation of the line for 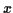 , giving
, giving
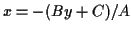 ,
and substituting this into the equation for the circle. Solving will
involve a quadratic equation, but the solution will at worst require
the quadratic formula, and thus a square root of some numbers we
already have. Note that there are two, one, or zero roots, depending
on whether the line cuts the circle, is tangent to it, or misses it
entirely.
,
and substituting this into the equation for the circle. Solving will
involve a quadratic equation, but the solution will at worst require
the quadratic formula, and thus a square root of some numbers we
already have. Note that there are two, one, or zero roots, depending
on whether the line cuts the circle, is tangent to it, or misses it
entirely.
- Finally, we need to be able to find the intersections of
two circles. In this case, suppose that the equations of the two
circles are given by:
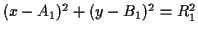 and
and
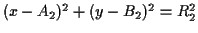 . But if you multiply these out,
you get two eqauations that look like this:
. But if you multiply these out,
you get two eqauations that look like this:
If you subtract them, you can see that the system above is equivalent,
algebraically, to the system:
This can be solved exactly as we did in the line-circle case, giving
up to two solutions, and requiring nothing more than a square root in
the quadratic formula.
So if you look at the algebraic result of any of the above constructions,
you can see that nothing is much worse than a combination of addition,
subtraction, multiplication, division, and square roots of the numbers
(coordinates) you started with before the construction.
It is also not hard to show that any such arithmetic operation can be
emulated with a proper geometric construction, so all of those sorts of
numbers (coordinates) can be constructed. So here's the idea of where
you can get after a certain number of steps, beginning only with the
number 1:
- You can make all the integers:
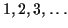 .
.
- You can make all the fractions (usually called ``rational
numbers'':
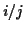 , where
, where 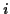 and
and 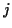 are integers.
are integers.
- You can make anything that looks like
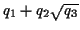 , where
, where
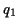 ,
, 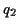 and
and 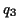 are any rational number.
are any rational number.
- You can make anything that looks like
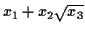 , where
, where
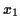 ,
, 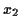 and
and 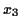 are any numbers you generate in step 3.
are any numbers you generate in step 3.
- You can make anything that looks like
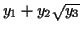 , where
, where
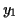 ,
, 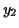 and
and 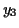 are any numbers you generate in step 4.
are any numbers you generate in step 4.
- You can make anything that looks like
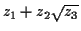 , where
, where
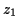 ,
, 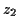 and
and 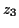 are any numbers you generate in step 5.
are any numbers you generate in step 5.
- Et cetera...
Thus, numbers like the following are ``easily'' obtainable:
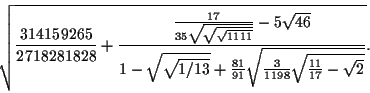 |
(1) |
Another way of looking at it is that any number that can be expressed
as a ``tower'' of square roots and arithmetic operations can be constructed
with a straightedge and compass.
But let's look at an example that's a little simpler than
expression 1, above. Consider:
where we've called the constructed number 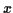 .
.
The equation above can be converted as follows:
The final equation above is just (if you multiply it out) an equation
containing powers of 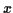 that are powers of 2, and exactly the same
thing can be done with any such constructable number.
that are powers of 2, and exactly the same
thing can be done with any such constructable number.
It may be obvious (but it certainly requires proof, and the proof is
beyond the scope of this paper) that no matter how many square roots
you apply, you can never get to a cube root (or a fifth root, or sixth
root, or seventh root, or ninth root...). So if the number you
would like to construct involves a cube root (or fifth root, or sixth
root, ...), you are out of luck--it cannot be constructed using
the methods described in Section 3.



Next: Three Impossible Constructions
Up: Algebraic Equivalent
Previous: Arithmetic Exercises
Zvezdelina Stankova-Frenkel
2000-11-13
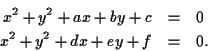
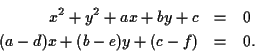
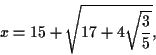
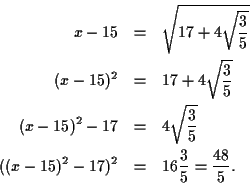
![]() that are powers of 2, and exactly the same
thing can be done with any such constructable number.
that are powers of 2, and exactly the same
thing can be done with any such constructable number.