Diophantine equations

One important use of algebraic numbers is to answer questions about Diophantine equations. We have already seen one example of this (representing an integer as the sum of two squares); let's consider a few more examples. The equation $x^2 - Dy^2=1$ is (mis)named ``Pell's equation''. Over $\mathbb{Q}(\sqrt{-D})$, we can factor the left side and rewrite the equation as

$$(x+y\sqrt{D})(x - y \sqrt{D}) = 1.$$

This makes clear the multiplicative structure of the set of solutions: if $(a,b)$ and $(c,d)$ are solutions, then

$$1 = (a+b\sqrt{D})(c+d\sqrt{D})(a-b\sqrt{D})(c-d\sqrt{D})$$

$$= [(ac+bdD)+(ad+bc)\sqrt{D}][(ac+bdD)-(ad+bc)\sqrt{D}]$$

$$= (ac+bdD)^2 - D(ad+bc)^2.$$

Moreover, we can sort all solutions into increasing order by $x+y\sqrt{D}$ (which is an increasing function of $x$ for $x\geq 0$, given that $x^2 - Dy^2=1$). Now it's easy to see that all solutions in positive integers are ``powers'' of the smallest solution, assuming that any solutions exist. There are several ways to show that solutions exist. One method uses continued fractions and has been known at least for 1000 years (it occurs in an old Indian text); it is probably the best method for explicitly computing solutions. ASIDE: What does this have to do with algebraic numbers? What we've done is to classify the algebraic integers in the field $\mathbb{Q}(\sqrt{D})$ whose products with their conjugates equal 1. An analogous classification can be made for an arbitrary number field, which solves the Pell equation along the way. What about the equation $x^2-Dy^2=n$ when $n \neq 1$? The situation is more complicated, so one needs to know a bit more to make progress. For example, given that $\mathbb{Q}(\sqrt{2})$ has unique factorization, one can prove the following. (Note the resemblance to the proof that a prime $p \equiv 1 \pmod{4}$ is the sum of two squares.)

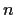
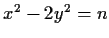
Theorem 6   For $n$ a squarefree integer, the equation $x^2-2y^2=n$ has a solution in integers if and only if it has a solution modulo $n$.

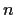
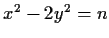
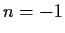
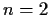
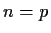
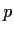
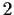
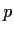
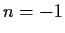
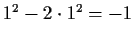
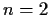
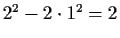
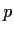
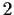
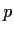
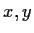
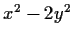
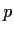
Proof. By multiplicativity, it suffices to show that $x^2-2y^2=n$ has a solution for $n=-1$, $n=2$, and $n=p$ for $p$ an odd prime such that $2$ is congruent to a square modulo $p$. For $n=-1$, use $1^2-2\cdot 1^2=-1$; for $n=2$, use $2^2 - 2\cdot 1^2 = 2$. Now suppose $p$ is an odd prime such that $2$ is congruent to a square modulo $p$. 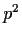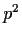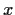Find $x,y$ such that $x^2-2y^2$ is divisible by $p$ but not by $p^2$ (if it is divisible by $p^2$, fix that by replacing $x$ with $x+p$). 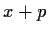Now form the ideal $(x+y\sqrt{D}, p)$. 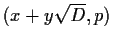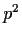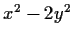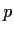Its norm divides $p^2$ and $x^2-2y^2$, so it must be $p$. $\qedsymbol$

Incidentally, one can replace 2 by any integer $D$ such that $\mathbb{Q}(\sqrt{D})$ has unique factorization, provided that $x^2-Dy^2=-1$ has a solution. It turns out (but is by no means obvious!) that unique factorization implies that $D$ is prime, and it is believed (but not proved) that $\mathbb{Q}(\sqrt{D})$ has unique factorization for about $75\%$ of the primes $D$. Moreover, existence of a solution of $x^2 - Dy^2=1$ then implies $D \equiv 1 \pmod{4}$, but not every prime congruent to 1 modulo 4 will work (try $D=5$). For an example of a different flavor, let us find the solutions of the equation $x^2+2=y^3$. In the ring $\mathbb{Z}[\sqrt{-2}]$, which has unique factorization, this factors as

$$(x+\sqrt{-2})(x - \sqrt{-2}) = y^3.$$

Note that $x$ must be odd: if $x$ were even, then $x^2+2$ would be divisible by 2 but not by 4, so could not be a perfect cube. Therefore the ideals $(x+\sqrt{-2})$ and $(x-\sqrt{-2})$ are relatively prime, and each must be the cube of an ideal. That is, $x + \sqrt{-2}$ and $x - \sqrt{-2}$ are equal to a unit (which can only be $\pm 1$) times a a cube. In particular, we have

$$x + \sqrt{-2} = (a+b\sqrt{-2})^3 = (a^3-6ab^2) + (3a^2 b - 2b^3) \sqrt{-2}.$$

In particular, $3a^2 b - b^3 = 1$. Since this is a multiple of $b$, we must have $b = \pm 1$. If $b=1$, then $3a^2-2 = 1$, so $a=1$ and $x= 5$. If $b=-1$, then $-3a^2+2=1$, which is impossible. ASIDE: We didn't actually need unique factorization: the argument still would go through if we just knew that the number field had class number not divisible by 3. Additional examples:

1. One can prove the law of quadratic reciprocity by working with number fields containing roots of unity. (Quadratic reciprocity will be described in Oaz's talk.)
2. Lamé gave a proof of Fermat's Last Theorem for $p$-th powers assuming that the number field $\mathbb{Q}(e^{2\pi i/p})$ has unique factorization. Unfortunately, this only holds for finitely many primes $p$. Fortunately, Kummer gave a proof that also works if the class number of $\mathbb{Q}(e^{2\pi i/p})$ is not divisible by $p$. Unfortunately, no one has proved that there are infinitely many such $p$. Fortunately, numerical evidence and heuristics suggest that about $60\%$ of primes have this property. (More fortunately, Fermat's Last Theorem has now been proved by Wiles et al.)