


Next: Inhomogeneous recurrence relations
Up: Linear recursive sequences
Previous: Example: the formula for
Let
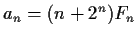 , where
, where 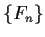 is the Fibonacci sequence.
Then by the explicit formula for
is the Fibonacci sequence.
Then by the explicit formula for 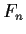 ,
,
By Theorem 1, 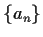 satisfies a linear recurrence with
characteristic polynomial
satisfies a linear recurrence with
characteristic polynomial
where we have used the identity
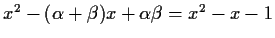 to compute
to compute
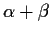 and
and
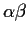 .
In other words,
for all
.
In other words,
for all 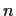 .
In fact, we have found the minimal characteristic polynomial,
since if the actual minimal characteristic polynomial
were a proper divisor of
.
In fact, we have found the minimal characteristic polynomial,
since if the actual minimal characteristic polynomial
were a proper divisor of
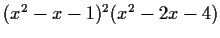 ,
then according to Theorem 1,
the explicit formula for
,
then according to Theorem 1,
the explicit formula for 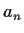 would have had a different, simpler form.
would have had a different, simpler form.



Next: Inhomogeneous recurrence relations
Up: Linear recursive sequences
Previous: Example: the formula for
Zvezdelina Stankova-Frenkel
2000-09-20
![]() , where
, where ![]() is the Fibonacci sequence.
Then by the explicit formula for
is the Fibonacci sequence.
Then by the explicit formula for ![]() ,
,
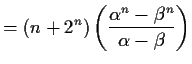
![$\displaystyle = \left[ \left( \frac{1}{\alpha-\beta} \right) n \right] \alpha^n...
...\beta} \right) (2\alpha)^n + \left( \frac{-1}{\alpha-\beta} \right) (2\beta)^n.$](img118.gif)