- If the Fibonacci sequence is extended to a doubly infinite sequence
satisfying the same linear recurrence,
then what will
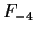 be?
(Is it easier to do this using the recurrence,
or using the explicit formula?)
be?
(Is it easier to do this using the recurrence,
or using the explicit formula?)
- Find the smallest degree polynomial that could be the minimal characteristic
polynomial of a sequence that begins
Assuming that the sequence is a linear recursive sequence
with this characteristic polynomial,
find an explicit formula for the 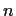 -th term.
-th term.
- Suppose that
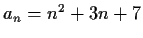 for
for 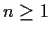 .
Prove that
.
Prove that 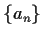 is a linear recursive sequence,
and find its minimal characteristic polynomial.
is a linear recursive sequence,
and find its minimal characteristic polynomial.
- Suppose
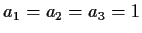 ,
, 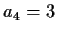 , and
, and
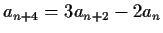 for
for 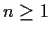 .
Prove that
.
Prove that 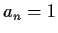 if and only if
if and only if 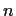 is odd or
is odd or 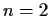 .
(This is an instance of the Mahler-Lech theorem:
for this sequence, one would take
.
(This is an instance of the Mahler-Lech theorem:
for this sequence, one would take 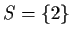 and
and
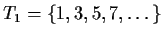 .)
.)
- Suppose
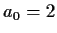 ,
, 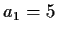 , and
, and
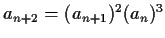 for
for 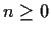 .
(This is a recurrence relation, but not a linear recurrence relation.)
Find an explicit formula for
.
(This is a recurrence relation, but not a linear recurrence relation.)
Find an explicit formula for 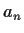 .
.
- Suppose
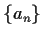 is a sequence such that
is a sequence such that
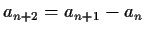 for all
for all 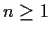 .
Given that
.
Given that 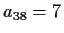 and
and 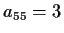 , find
, find 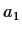 .
(Hint: it is possible to solve this problem with very little calculation.)
.
(Hint: it is possible to solve this problem with very little calculation.)
- Let
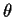 be a fixed real number,
and let
be a fixed real number,
and let
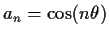 for integers
for integers 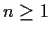 .
Prove that
.
Prove that 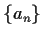 is a linear recursive sequence,
and find the minimal characteristic polynomial.
(Hint: if you know the definition of
is a linear recursive sequence,
and find the minimal characteristic polynomial.
(Hint: if you know the definition of 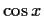 in terms of complex
exponentials, use that.
Otherwise, use the sum-to-product rule for the sum of cosines
in terms of complex
exponentials, use that.
Otherwise, use the sum-to-product rule for the sum of cosines
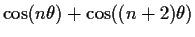 .
For most but not all
.
For most but not all 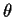 ,
the degree of the minimal characteristic polynomial will be 2.)
,
the degree of the minimal characteristic polynomial will be 2.)
- Give an example of a sequence that is not
a linear recursive sequence, and prove that it is not one.
- Given a finite set
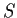 of positive integers, show that there
exists a linear recursive sequence
of positive integers, show that there
exists a linear recursive sequence
such that
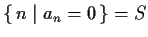 .
.
- A student tosses a fair coin and scores one point for each head
that turns up, and two points for each tail.
Prove that the probability of the student scoring
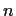 points
at some time in a sequence of
points
at some time in a sequence of 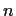 tosses is
tosses is
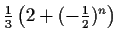 .
.
- Let
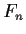 denote the
denote the 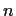 -th Fibonacci number.
Let
-th Fibonacci number.
Let
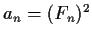 .
Prove that
.
Prove that
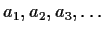 is a linear recursive sequence,
and find its minimal characteristic polynomial.
is a linear recursive sequence,
and find its minimal characteristic polynomial.
- Prove the ``fact from algebra'' mentioned above in Section 5.
(Hint: if
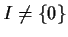 ,
pick a nonzero polynomial in
,
pick a nonzero polynomial in 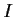 of smallest degree,
and multiply it by a constant to get a monic polynomial
of smallest degree,
and multiply it by a constant to get a monic polynomial 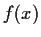 .
Use long division of polynomials to show that anything else in
.
Use long division of polynomials to show that anything else in 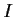 is a polynomial multiple of
is a polynomial multiple of 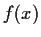 .)
.)
- Suppose that
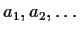 is a linear recursive sequence.
For
is a linear recursive sequence.
For 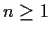 , let
, let
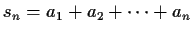 .
Prove that
.
Prove that 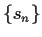 is a linear recursive sequence.
is a linear recursive sequence.
- Suppose
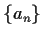 and
and 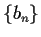 are linear recursive sequences.
Let
are linear recursive sequences.
Let
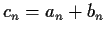 and
and
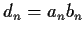 for
for 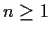 .
.
(a) Prove that 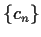 and
and 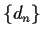 also are linear recursive sequences.
also are linear recursive sequences.
(b) Suppose that the minimal characteristic polynomials for
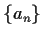 and
and 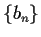 are
are 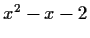 and
and 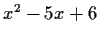 , respectively.
What are the possibilities
for the minimal characteristic polynomials of
, respectively.
What are the possibilities
for the minimal characteristic polynomials of 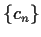 and
and 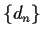 ?
?
- Suppose that
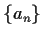 and
and 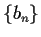 are linear recursive sequences.
Prove that
also is a linear recursive sequence.
are linear recursive sequences.
Prove that
also is a linear recursive sequence.
- Use the Mahler-Lech theorem to prove the following generalization.
Let 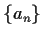 be a linear recursive sequence
of complex numbers, and let
be a linear recursive sequence
of complex numbers, and let 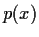 be a polynomial.
Then there exists a finite (possibly empty) list of arithmetic progressions
be a polynomial.
Then there exists a finite (possibly empty) list of arithmetic progressions
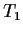 ,
, 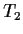 , ...
, ...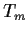 and a finite (possibly empty) set
and a finite (possibly empty) set 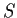 of integers
such that
of integers
such that
(Hint: let
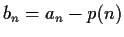 .)
.)
- (1973 USAMO, no. 2)
Let
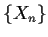 and
and 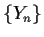 denote two sequences of integers defined
as follows:
Thus, the first few terms of the sequences are:
Prove that, except for the ``1,'' there is no term which occurs
in both sequences.
denote two sequences of integers defined
as follows:
Thus, the first few terms of the sequences are:
Prove that, except for the ``1,'' there is no term which occurs
in both sequences.
- (1963 IMO, no. 4)
Find all solutions
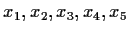 to the system
to the system
where 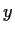 is a parameter.
(Hint: define
is a parameter.
(Hint: define 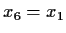 ,
, 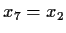 , etc., and find two different
linear recurrences satisfied by
, etc., and find two different
linear recurrences satisfied by 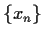 .)
.)
- (1967 IMO, no. 6)
In a sports contest,
there were
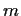 medals awarded on
medals awarded on 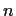 successive days (
successive days (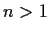 ).
On the first day,
one medal and
).
On the first day,
one medal and 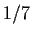 of the remaining
of the remaining 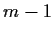 medals were awarded.
On the second day,
two medals and
medals were awarded.
On the second day,
two medals and 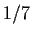 of the now remaining medals were awarded; and so on.
On the
of the now remaining medals were awarded; and so on.
On the 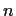 -th and last day, the remaining
-th and last day, the remaining 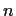 medals were awarded.
How many days did the contest last,
and how many medals were awarded altogether?
medals were awarded.
How many days did the contest last,
and how many medals were awarded altogether?
item
(1974 IMO, no. 3)
Prove that the number
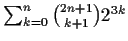 is not divisible by 5 for any integer
is not divisible by 5 for any integer 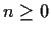 .
.
- (1980 USAMO, no. 3)
Let
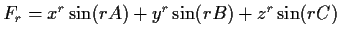 ,
where
,
where
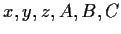 are real and
are real and 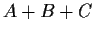 is an integral multiple of
is an integral multiple of 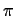 .
Prove that if
.
Prove that if 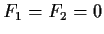 , then
, then 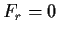 for all positive integral
for all positive integral 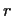 .
.
![]() .
.
![]() and
and ![]() also are linear recursive sequences.
also are linear recursive sequences.
![]() and
and ![]() are
are ![]() and
and ![]() , respectively.
What are the possibilities
for the minimal characteristic polynomials of
, respectively.
What are the possibilities
for the minimal characteristic polynomials of ![]() and
and ![]() ?
?
![]() be a linear recursive sequence
of complex numbers, and let
be a linear recursive sequence
of complex numbers, and let ![]() be a polynomial.
Then there exists a finite (possibly empty) list of arithmetic progressions
be a polynomial.
Then there exists a finite (possibly empty) list of arithmetic progressions
![]() ,
, ![]() , ...
, ...![]() and a finite (possibly empty) set
and a finite (possibly empty) set ![]() of integers
such that
of integers
such that
![]() is not divisible by 5 for any integer
is not divisible by 5 for any integer ![]() .
.