This Talk is Under Construction
Berkeley Math Circle 2001-2002
Kiran Kedlaya
The straightedge and compass operations.
- (a)
- Given two points, we may construct the line through them.
- (b)
- Given two points, we may construct the circle centered at one point passing
through the other point.
- (c)
- Given two lines, two circles, or a line and a circle, we may construct
their intersection points.
Recall some things you can construct from these steps:
- the perpendicular bisector of the segment joining two points;
- the angle bisectors of two given lines;
- the circle through three given points;
- a segment of length
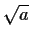 , given segments of length 1 and
, given segments of length 1 and 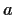 ;
;
- the regular hexagon, pentagon and 17-gon (!);
and some things you've probably heard cannot be constructed from these steps:
- the trisectors of an arbitrary angle;
- a regular heptagon (7-gon) or nonagon (9-gon);
- a segment of length
![$ \sqrt[3]{2}$](img3.png) , given segments of length
, given segments of length 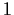 and
and 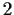 .
.
We call a real number 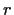 (straightedge and compass) constructible
if, starting from two points
at distance 1, we can produce two more points at distance
(straightedge and compass) constructible
if, starting from two points
at distance 1, we can produce two more points at distance 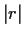 by a finite
sequence of straightedge and compass operations. We call a complex
number constructible if its real and imaginary parts are constructible.
Then:
by a finite
sequence of straightedge and compass operations. We call a complex
number constructible if its real and imaginary parts are constructible.
Then:
- the number 1 is constructible;
- if
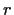 and
and 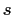 are constructible, then so are
are constructible, then so are 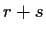 ,
,  , and
, and 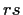 ;
;
- if
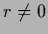 is constructible, so is
is constructible, so is 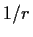 ;
;
- if
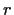 is constructible, so are
is constructible, so are
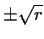 ;
;
- a number
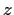 is constructible if and only if it can be written in
terms of rational numbers using only addition, subtraction, multiplication,
division and square roots.
is constructible if and only if it can be written in
terms of rational numbers using only addition, subtraction, multiplication,
division and square roots.
In particular, each constructible number is algebraic: it is the root
of some polynomial with integer coefficients. A famous theorem of Lindemann
states that 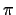 is transcendental (not algebraic); that's why one cannot
``square the circle''. But there are algebraic numbers that are not
constructible, such as
is transcendental (not algebraic); that's why one cannot
``square the circle''. But there are algebraic numbers that are not
constructible, such as
![$ \sqrt[3]{2}$](img3.png) .
.
Warning. The next part of the discussion belongs to the subject of
abstract algebra, so may involve some ideas you may not have seen before;
but I hope the intuition will be clear.
(A subset of that is what is called ``linear algebra''; that's pretty much
all I'm really using.)
Given a finite set 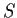 of algebraic numbers, the set of complex numbers
obtained from
of algebraic numbers, the set of complex numbers
obtained from 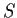 and the rational numbers
by addition, subtraction, multiplication and division forms what is called a
number field. If
and the rational numbers
by addition, subtraction, multiplication and division forms what is called a
number field. If 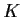 is a number field, we can always find
is a number field, we can always find
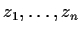 in
in 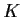 such that
such that
and that representation is not redundant (there's only way to write any
element of 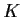 this way). Such a set
this way). Such a set
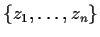 is called a
basis of
is called a
basis of 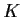 , and the number
, and the number 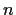 turns out not to depend on the
choice of the basis
(a fact from linear algebra that I'm not going to prove now).
That number is called the degree of the number field. For example,
the number field
turns out not to depend on the
choice of the basis
(a fact from linear algebra that I'm not going to prove now).
That number is called the degree of the number field. For example,
the number field 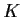 generated by
generated by
![$ \sqrt[3]{2}$](img3.png) has degree 3, because we can
take
has degree 3, because we can
take
![$ z_1 = 1, z_2 = \sqrt[3]{2}, z_3 = \sqrt[3]{4}$](img23.png) . And if
. And if 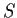 consists
of a single primitive
consists
of a single primitive 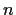 -th root of unity
-th root of unity
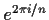 , then the degree
of
, then the degree
of 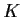 turns out to be the Euler phi function
turns out to be the Euler phi function 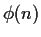 .
.
Theorem 1
If
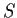
is a finite set of constructible numbers and
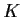
is the number field
they generate, then the degree of
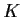
is a power of 2.
Proof.
[Sketch]
We prove this by induction on the size of
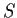
. It's obvious if
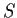
is
of size zero, since then
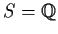
. Suppose
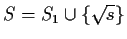
,
and assume
that the degree of the number field
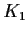
generated by
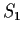
is a power
of 2 and that
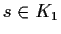
. If
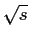
is already in
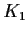
, then
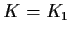
and we're done. Otherwise,
pick a basis
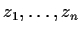
of
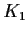
; then I claim that
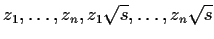
is a basis of
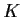
.
Certainly every element of
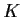
can be written as
with the
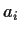
and
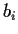
all rational. So we only have to check that there
aren't two ways to write some number; in fact, we only have to check that
there is no way to write 0 besides using all zeroes. If we had a nontrivial
way to write zero, we could write
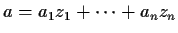
and
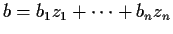
, which are both elements of
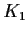
.
Then
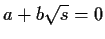
; if
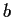
were nonzero, then
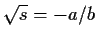
would be in
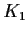
, contradiction. So

and hence
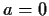
; but since
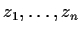
is a basis of
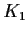
, this can only happen if the
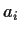
and
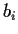
are all zero.
Conclusion: the degree of
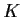
is exactly twice that of
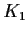
, so it's also
a power of 2.
Why this is only a sketch: You can always arrange for this
induction to work at the cost of making
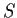
larger. (Given whatever numbers
you started with, you have to toss in the ``intermediate'' numbers you
needed to construct them.) So you have to check that if the degree of a
number field is a power of 2, then the degree of any number field
it contains is also a power of 2, which requires a little more linear
algebra.

So for example,
![$ \sqrt[3]{2}$](img3.png) is not constructible, because the number field
it generates has degree 3. Also,
is not constructible, because the number field
it generates has degree 3. Also,
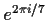 and
and
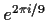 both
generate number fields of degree 6, so they're not constructible either;
thus the regular 7-gon and 9-gon cannot be constructed with straightedge
and compass!
It turns out the converse is also true: if an algebraic number generates a
number field whose degree is a power of 2, then it is constructible. I won't
prove this, but I'll give you an example. A 17-th root of unity
both
generate number fields of degree 6, so they're not constructible either;
thus the regular 7-gon and 9-gon cannot be constructed with straightedge
and compass!
It turns out the converse is also true: if an algebraic number generates a
number field whose degree is a power of 2, then it is constructible. I won't
prove this, but I'll give you an example. A 17-th root of unity
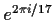 generates a number field of degree 16, so this converse says that a regular
17-gon is constructible. That is, we can write
generates a number field of degree 16, so this converse says that a regular
17-gon is constructible. That is, we can write
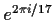 in terms
of rational numbers using square roots. We'll do that in the next section.
One can do likewise for a 65537-gon, since 65537 is prime and
in terms
of rational numbers using square roots. We'll do that in the next section.
One can do likewise for a 65537-gon, since 65537 is prime and
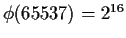 ; we won't do this here.
; we won't do this here.
Example: constructing the 17-gon.
In case you've never seen the construction of the 17-gon (due to Gauss), it's
worth a look, in part because it's a very simple example of a notion
from abstract algebra called a ``Galois group''.
Here's the idea: let
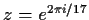 be a primitive 17th root of unity.
Note that
be a primitive 17th root of unity.
Note that 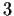 is a primitive root modulo 17, so that
is a primitive root modulo 17, so that
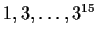 cover all the nonzero residue classes modulo 17. Now write
cover all the nonzero residue classes modulo 17. Now write
Gauss realized that each 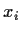 can be written as the root of a quadratic
polynomial in terms of the previous ones. I'll leave it to you to check
my arithmetic:
can be written as the root of a quadratic
polynomial in terms of the previous ones. I'll leave it to you to check
my arithmetic:
How do you guess this? I don't know how Gauss did it, but they are predicted
by Galois theory. That's the branch of mathematics that tells us that
you can't write the roots of a general degree 5 polynomial in terms of
the coefficients using addition, subtraction, multiplication, division, and
taking 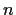 -th roots (the way the quadratic formula does this in degree 2,
and analogous formulas are known in degree 3 and 4).
Here's how the prediction is made in that language: the Galois group of
the number field generated by
-th roots (the way the quadratic formula does this in degree 2,
and analogous formulas are known in degree 3 and 4).
Here's how the prediction is made in that language: the Galois group of
the number field generated by 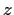 is a cyclic group of order 16, generated by
the map
is a cyclic group of order 16, generated by
the map 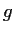 that sends
that sends 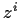 to
to 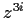 . (The point is that this map preserves
addition and multiplication, since all it's doing is changing from one
17-th root of unity to another.) The map
. (The point is that this map preserves
addition and multiplication, since all it's doing is changing from one
17-th root of unity to another.) The map 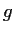 fixes only rational numbers;
the maps
fixes only rational numbers;
the maps 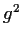 ,
, 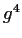 ,
, 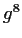 fix number fields of degree 2, 4, 8, respectively.
The image of
fix number fields of degree 2, 4, 8, respectively.
The image of 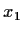 under
under 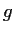 is precisely
is precisely 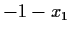 , so the product
, so the product
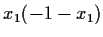 is fixed by
is fixed by 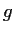 and so must be some rational number.
Likewise, the image of
and so must be some rational number.
Likewise, the image of 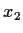 under
under 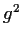 is
is 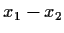 , so the product
, so the product
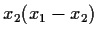 is fixed by
is fixed by 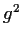 and so must be in the number field generated
by
and so must be in the number field generated
by 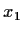 , and so forth.
, and so forth.
The marked straightedge operations.
In using the marked straightedge to trisect angles, Archimedes assumed an
additional axiom: (here 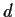 is the length marked on the straightedge)
is the length marked on the straightedge)
- (d)
- Given a line
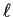 , a circle
, a circle 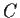 , and a point
, and a point 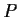 ,
we can construct
all pairs of points
,
we can construct
all pairs of points 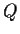 and
and 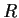 , with
, with 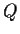 on
on 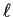 and
and 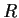 on
on 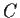 ,
such that the line
,
such that the line 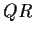 passes through
passes through 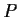 and the
distance
and the
distance 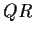 is equal to
is equal to 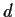 .
.
But you might as well go a little further, replacing the line 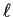 by
another circle:
by
another circle:
- (e)
- Given circles
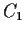 and
and 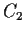 and a point
and a point 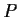 ,
we can construct
all pairs of points
,
we can construct
all pairs of points 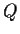 and
and 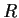 , with
, with 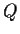 on
on 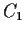 and
and 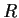 on
on 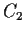 ,
such that the line
,
such that the line 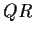 passes through
passes through 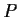 and the
distance
and the
distance 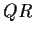 is equal to
is equal to 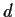 .
.
We can define marked straightedge constructible real and complex
numbers as you might expect, but the definition will depend on the distance
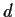 between the marks on the straightedge. The ``right'' definition is
to take
between the marks on the straightedge. The ``right'' definition is
to take 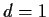 , the same as the distance between the two starting points. (Or
if you like, just take one starting point, and use the marked straightedge
to produce the second one!)
, the same as the distance between the two starting points. (Or
if you like, just take one starting point, and use the marked straightedge
to produce the second one!)
The ``solid'' operations.
The ancient Greeks considered a geometric object to be ``solid'' constructible
if if could be obtained using the ordinary straightedge and compass operations
plus the ability to draw conic sections. One can phrase this as follows:
- (d)
- Given five points, we may construct the conic section (parabola, hyperbola,
ellipse, or degenerate conic) through them.
- (e)
- Given a conic section and a line, circle or another conic, we may construct
their intersection points.
Likewise, one can define solid constructible real and complex numbers.
It turns out that a complex number 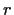 is constructible if and only if:
is constructible if and only if:
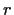 is algebraic, i.e.,
is algebraic, i.e., 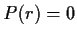 for some polynomial
for some polynomial 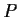 with
integer coefficients;
with
integer coefficients;
- for some such
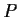 , the number field generated by all of the roots
of
, the number field generated by all of the roots
of 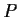 has degree a power of 2 times a power of 3. (It's enough to check
this for the polynomial
has degree a power of 2 times a power of 3. (It's enough to check
this for the polynomial 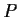 of smallest degree, called the minimal
polynomial of
of smallest degree, called the minimal
polynomial of 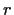 .)
.)
Warning: the second condition is stronger than saying that the number
field generated by 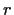 alone has degree a power of 2 times a power of 3.
For example, if
alone has degree a power of 2 times a power of 3.
For example, if 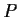 is a ``general'' polynomial of degree 6 with integer
coefficients, then the number field generated by
is a ``general'' polynomial of degree 6 with integer
coefficients, then the number field generated by 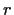 itself will have degree
6 but the number field generated by all of the roots of
itself will have degree
6 but the number field generated by all of the roots of 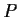 will have
degree
will have
degree 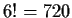 , which has the bad prime factor 5.
For a nice exposition of this, see the article ``Constructions Using a
Compass and Twice-Notched Straightedge'' by Arthur Baragar, in the February
2002 American Mathematical Monthly. He also includes a discussion of
the marked straightedge case, but a precise characterization of the
constructible numbers in that case is still unknown.
, which has the bad prime factor 5.
For a nice exposition of this, see the article ``Constructions Using a
Compass and Twice-Notched Straightedge'' by Arthur Baragar, in the February
2002 American Mathematical Monthly. He also includes a discussion of
the marked straightedge case, but a precise characterization of the
constructible numbers in that case is still unknown.
The origami operations.
The Japanese art of paper folding gives an entirely different approach to
constructing geometric figures. Here is one set of axioms for ``origami
geometry''; there may be others in the literature. (This one is from an
``origami mathematics'' web site.)
- (a)
- Given two points, we may construct the line through them.
- (b)
- Given two points, we may construct the perpendicular bisector of the segment
joining the two points (i.e., we may fold one point onto another).
- (c)
- Given two lines, we may form the angle bisector of either angle between them
(i.e, we may fold one line onto another).
- (d)
- Given a line and a point, we may construct the perpendicular to the line
through the point.
- (e)
- Given points
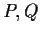 and a line
and a line 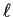 , we may construct the line
, we may construct the line 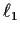 through
through 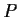 such that the reflection of
such that the reflection of 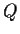 across
across 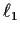 lies on
lies on 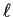 .
.
- (f)
- Given points
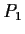 and
and 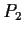 and lines
and lines 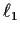 and
and 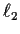 , we may
construct the line(s)
, we may
construct the line(s) 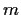 such that the reflection of
such that the reflection of 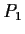 across
across
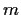 lies on
lies on 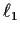 , and the reflection of
, and the reflection of 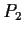 across
across 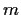 lies on
lies on 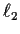 .
.
Challenge problems.
Some of these are discussed in the article by Baragar mentioned above,
which I again heartily recommend; he also includes many more challenge
problems. Warning: the characterizations of
constructible numbers involves the notion of a ``Galois group'', which
we haven't talked about.
- Find a construction of a regular 7-gon using marked straightedge.
- You might wonder why I didn't state a version of the marked straightedge
axiom (d) with two lines instead of a line and a circle. Prove that actually
the resulting construction can already done with straightedge and compass.
- Prove that origami constructions (a)-(e) can also be accomplished
with straightedge and compass. (The only subtle one is (e).)
- Find constructions for trisecting a given angle and doubling a cube
using origami. (This will imply that origami construction (f) cannot be
accomplished with straightedge and compass.)
- Find a regular polygon that cannot be constructed using origami.
Even better, find a characterization of origami constructible numbers.
(I believe the latter is unsolved!)
![]() of algebraic numbers, the set of complex numbers
obtained from
of algebraic numbers, the set of complex numbers
obtained from ![]() and the rational numbers
by addition, subtraction, multiplication and division forms what is called a
number field. If
and the rational numbers
by addition, subtraction, multiplication and division forms what is called a
number field. If ![]() is a number field, we can always find
is a number field, we can always find
![]() in
in ![]() such that
such that
![]() be a primitive 17th root of unity.
Note that
be a primitive 17th root of unity.
Note that ![]() is a primitive root modulo 17, so that
is a primitive root modulo 17, so that
![]() cover all the nonzero residue classes modulo 17. Now write
cover all the nonzero residue classes modulo 17. Now write
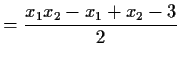
![]() is the length marked on the straightedge)
is the length marked on the straightedge)