Fixed Points and Fair Divisions
Berkeley Math Circle, November 11, 2001
Kiran S. Kedlaya (Berkeley)
Caution: these notes were originally written for
graduate students, so you may find them tough reading at first. Hopefully
this will be a lot less true by the end of the talk!
What do these two facts have in common?
- (a)
- If one copy of a map is crumpled up and placed on top of
a second, uncrumpled copy of the map, then there is a location whose
image on the crumpled map lies directly over its image on the
uncrumpled map.
- (b)
- Any group of people can divide a cake amongst themselves
so that each person believes her piece is the biggest.
The former is of course the Brouwer Fixed-Point Theorem (in two
dimensions), while the latter is known to some economists as the Fair
Division Theorem (or more precisely, the Envy-Free Fair Division
Theorem). The overt purpose of this talk is to illustrate the close
relationship between these two results, and in particular their common
genesis from a combinatorial result known as Sperner's Lemma. The secret purpose
is to motivate people to think more about this connection, since at present it
lacks a certain ``naturality'' that I think is hidden somewhere, and ought to be
brought to the fore.
Advertisement: the entire contents of this talk are shamelessly
lifted from the article ``Rental Harmony: Sperner's Lemma in Fair
Division'' by Francis Su, in the December 1999 American
Mathematical Monthly, pp. 930-942. You can play around with the fair
division algorithms in this talk using a Java applet at his web site:
http://www.math.hmc.edu/~su/fairdivision/
Before proceeding, let us fix some definitions. The simplex in
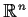 is the set
is the set
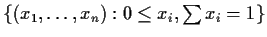 . We number the vertices so that vertex
. We number the vertices so that vertex  is the one with nonzero
is the one with nonzero
 -th coordinate.
The facets of this simplex are its intersections with
its supporting hyperplanes; a codimension 1 facet is also called a face.
We number the faces so face
-th coordinate.
The facets of this simplex are its intersections with
its supporting hyperplanes; a codimension 1 facet is also called a face.
We number the faces so face 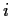 is opposite vertex
is opposite vertex 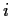 .
A triangulation of the simplex is
a covering of the simplex with subsimplices, such that if two subsimplices intersect,
their intersection is a
.
A triangulation of the simplex is
a covering of the simplex with subsimplices, such that if two subsimplices intersect,
their intersection is a 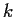 -facet of each of the two, for some
-facet of each of the two, for some 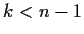 .
.
Lemma 1 (Sperner's Lemma)
Consider a triangulation of the simplex in
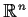
,
whose subvertices are each labeled with
one of
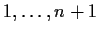
, subject to the restriction that each subvertex
lying on the facet of the simplex with vertices
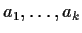
is itself labeled with one of
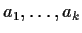
. Then
the number of subsimplices whose subvertices are labeled
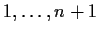
is odd and thus nonzero. (If counted with
orientation, the number is equal to
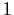
.)
We defer the proof for the time being. For now, let us see how this
lemma implies both the Fixed Point Theorem and the Fair Division
Theorem.
Theorem 1 (Fixed Point Theorem)
Any continuous map from the simplex in
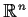
to itself has a fixed point.
Proof.
[Proof of the Fixed Point Theorem.]
For
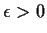
, construct a triangulation such that no two
points within a subsimplex have any coordinate differing by
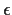
or greater, or map to points with any coordinate
differing by
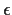
or
greater. Label each subvertex
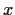
with a number
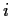
such
that the
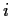
-th coordinate of
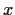
is nonzero, and is greater than or
equal to the
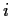
-th coordinate of
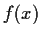
.
This labeling is a Sperner labeling: on
the facet with vertices
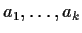
, only these coordinates
are nonzero. Thus there
exists a subsimplex labeled
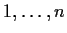
. No point in this subsimplex
can move to a point with a coordinate increased by
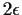
or
more, since there is a point in the simplex for which this coordinate
decreases.
By compactness,
there is a sequence of
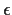
tending to 0 whose corresponding
subsimplices have nonempty intersection. Any point in this
intersection must map to itself (since none of its coordinates can
increase by more than
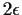
for arbitrarily small
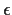
).

Theorem 2 (Envy-Free Fair Division Theorem)
Consider a one-dimensional cake to be divided into
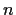
pieces by
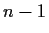
cuts. From each possible division, each of
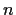
players designates one
or more pieces as ``preferred''. These preferences obey the following rules:
- (a)
- Continuity: If a player prefers a piece in each of a set
of divisions, he prefers that piece in each limiting division.
- (b)
- Boundary condition: No player ever prefers an empty piece.
Then there exists a division and an assignment of each piece to a
different player, such that each player receives one of his preferred
pieces.
Beware that the well-known ``moving-knife'' method does not suffice to prove this result.
In that method, a knife is drawn sideways across the cake; as soon as a player
believes the knife has covered 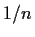 of the cake, he signals the knife-mover to
cut and takes the resulting piece. The remaining players then repeat the procedure
until each player receives a piece. This method guarantees that each player
receives at least
of the cake, he signals the knife-mover to
cut and takes the resulting piece. The remaining players then repeat the procedure
until each player receives a piece. This method guarantees that each player
receives at least 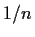 of the cake in his own measure (since he believes the pieces
cut off before the one he receives are smaller than
of the cake in his own measure (since he believes the pieces
cut off before the one he receives are smaller than 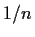 , so even if he gets the
last piece, it will have size at least
, so even if he gets the
last piece, it will have size at least 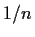 ).
There are two reasons why our result is stronger than that given by
the moving-knife method. First, our theorem does not assume that players' preferences
are given by measures on the cake. For example, if
).
There are two reasons why our result is stronger than that given by
the moving-knife method. First, our theorem does not assume that players' preferences
are given by measures on the cake. For example, if 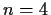 , a player could prefer
piece 1 in one division, and piece 2 in a division that differs from the first only
in the sizes of pieces 3 and 4! Second, even if the preferences are given by
measures, the moving-knife method only guarantees that a player receives a piece as
least as large as the average piece, and not necessarily the biggest piece (this is
why our theorem is called ``envy-free'').
, a player could prefer
piece 1 in one division, and piece 2 in a division that differs from the first only
in the sizes of pieces 3 and 4! Second, even if the preferences are given by
measures, the moving-knife method only guarantees that a player receives a piece as
least as large as the average piece, and not necessarily the biggest piece (this is
why our theorem is called ``envy-free'').
Proof.
[Proof of the Fair Division Theorem]
(due to Forest Simmons)
Identify the possible divisions with the simplex in
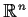
,
so that vertex
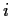
corresponds to all of the cake lying in piece
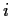
.
For
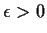
, construct a triangulation of the simplex such
that no two subvertices are at distance
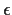
or greater, and
which can be labeled by the names of the players so that
each
subsimplex has subvertices labeled by the names of all of the players.
(Given a
triangulation satisfying the first condition, its barycentric
subdivision satisfies both conditions: for each of
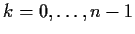
,
label all of the barycenters of
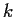
-simplices with a single player.)
Now
construct a second labeling of this triangulation as follows: for
each subvertex, query the player whose name labels that subvertex,
and label the subvertex with one of his preferred pieces in the
corresponding division. The result is a
Sperner labeling, since on the facet with vertices
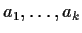
, only pieces
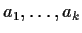
are nonempty, so only they
will be preferred. Thus there exists a subsimplex labeled
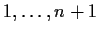
, which is to say, a subsimplex where each player chooses a
different piece at his corresponding subvertex.
By compactness (and the finiteness of the number of ways for the
players to choose pieces), there exists a sequence of
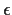
tending to 0 such that the corresponding subsimplices have
nonempty intersection, and such that each player chooses the same
piece each time his name occurs as the label of a subvertex.
A point in that intersection is a division in
which each player prefers a different piece, as desired.

Proof.
[Proof of Sperner's Lemma]
We proceed by induction on
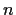
. By the induction hypothesis, the
face with vertices
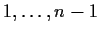
has been given a Sperner
labeling and so contains an odd number of subsimplices labeled
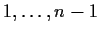
.
We refer to each subface labeled
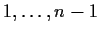
as a
door. We have just seen that there are an odd number of doors
on the boundary of the simplex. Moreover, each subsimplex
contains 1 door if it is labeled
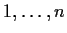
, and 0 or 2 doors
otherwise.
Now consider the graph on the subsimplices, which are considered
adjacent if they share a common subface which is also a door.
This graph is a disjoint set of paths of two types: those
starting and ending on the boundary, and those starting on the
boundary and ending at a subsimplex labeled
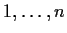
. Since each
path of the former type uses two boundary doors, there are an odd
number of the second type, and so an odd number of subsimplices labeled
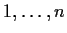
.

The algorithmic nature of this proof yields approximate algorithms
for finding fixed points and fair divisions.
The Fair Division Theorem concerns division of benefits. What about
the dual situation, where players must divide a certain cost? For
example, if 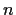 graduate students share an apartment, and decide to
divide the rent by room, can this division be set so that each
person will opt for a different room? As we shall see, Sperner's
lemma, or rather a dual incarnation of it, can answer this question as
well.
graduate students share an apartment, and decide to
divide the rent by room, can this division be set so that each
person will opt for a different room? As we shall see, Sperner's
lemma, or rather a dual incarnation of it, can answer this question as
well.
Theorem 3 (Rental Division Theorem)
Consider
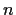
rooms and a total rent to be divided among the rooms.
For each such division, each of
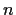
players designates one or more
rooms as ``preferred''. These
preferences obey the following rules:
- (a)
- Continuity: If a player prefers a piece in each of a set
of divisions, he prefers that piece in each limiting division.
- (b)
- Boundary condition: If there is a room with rent at most 0,
no player will prefer a room with positive rent.
Then there exists a division and an assignment of each room to a
different player, such that each player receives one of his preferred
rooms.
Lemma 2 (Dual Sperner's Lemma)
Consider a triangulation of the simplex in
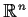
,
whose subvertices are each labeled with
one of
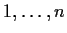
, subject to the restriction that each subvertex
lying on the intersection of faces
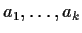
is itself labeled with one of
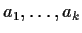
. Assume
moreover that each facet contains a subvertex in its interior. Then
the number of subsimplices whose vertices are labeled
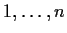
is odd and thus nonzero.
Proof.
[Proof of Dual Sperner's Lemma]
As in the proof of Sperner's Lemma, it suffices to show that the
number of doors on the
boundary of the simplex is odd. Note that a door must have at least
one subvertex on each of faces
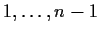
. This restriction,
together with the condition that the door lies on the boundary, forces
the vertex at the intersection of faces
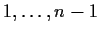
to be a
subvertex of the door. Without loss of generality suppose this vertex
is labeled
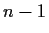
. Then of the other subvertices of the door, one must
lie on each of face
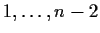
, and so the door must have a
second subvertex on the intersection of face
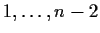
.
Repeating this argument shows that in fact there is exactly one door
on the boundary of the simplex. Thus there are an odd number of
subsimplices labeled
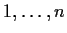
by the same argument as above.

Proof.
[Proof of the Rental Division Theorem]
Identify the possible divisions with the simplex in
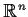
,
so that the
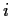
-th coordinate represents the price of room
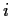
,
triangulated as in the proof of the Fair Division Theorem.
For
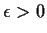
, construct a triangulation of the simplex such
that no two subvertices are at distance
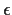
or greater, and which
can be labeled by the names of the players so that
each
subsimplex is labeled with the names of all of the players.
Now
construct a second labeling of this triangulation as follows: for
each subvertex, query the player whose name labels that subvertex,
and label the subvertex with one of that player's preferred rooms in
the corresponding division. This new labeling is a dual Sperner
labeling: on the intersection of facets
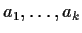
,
rooms
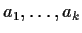
have zero rent and so no other rooms will
be preferred. Thus the Dual Sperner's Lemma implies the existence of
a subsimplex labeled
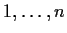
. The remainder of the argument
is the same as that of the Fair Division Theorem.

In conclusion, it should be noted that other results from topology
also yield fair division results, and more specifically results in combinatorial
topology yield approximate algorithms for fair division problems.
For example, the Borsuk-Ulam theorem
(any map from the 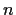 -sphere to
-sphere to
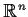 maps some pair of antipodal
points to the same point) yields the fact that a cake can be divided
in two so that each of
maps some pair of antipodal
points to the same point) yields the fact that a cake can be divided
in two so that each of 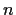 people prefers both pieces equally. (The
proof of the latter is similar to that of the Ham Sandwich Theorem.)
On the other hand, the correspondence between topology and fair division is
not completely understood; we have fragmentary results, but no unifying
treatment.
people prefers both pieces equally. (The
proof of the latter is similar to that of the Ham Sandwich Theorem.)
On the other hand, the correspondence between topology and fair division is
not completely understood; we have fragmentary results, but no unifying
treatment.