


Next: Algebraic Equivalent
Up: construct
Previous: Some Final Warnings
Here are a list of elementary constructions that can be carried out
with a straightedge and compass. They are arranged roughly in order
of difficulty, and if you can do most of these, you can do most
standard geometric constructions.
- Copy a segment. In other words, mark off a segment that
exactly matches the length of a given segment on a different
straight line.
- Copy an angle. Given an angle, make another angle of exactly
the same size somewhere else.
- Bisect a segment. This problem was already solved in
Section 1
- Bisect an angle. Given an angle, find a line through the
vertex that divides it in half.
- Construct a line perpendicular to a given line through a point
on the given line.
- Construct a line perpendicular to a given line and passing
through a point not on the given line.
- Given a line
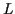 and a point
and a point 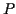 not on
not on 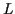 , construct a new
line that passes through
, construct a new
line that passes through 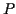 and is parallel to
and is parallel to 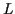 .
.
- Construct an angle whose size is the sum or difference of
two given angles.
- Given three segments, construct a triangle whose sides have the
same lengths as the segments.
- Construct the perpendicular bisector of a line segment.
- Given three points, construct the circle that passes through
all of them.
- Given a circle, find its center.
- Given a triangle
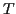 , construct the inscribed and circumscribed
circles. The inscribed circle is a circle that fits inside the
triangle and touches all three edges; the circumscribed circle is
outside the triangle except that it touches all three of the vertices
of the triangle.
, construct the inscribed and circumscribed
circles. The inscribed circle is a circle that fits inside the
triangle and touches all three edges; the circumscribed circle is
outside the triangle except that it touches all three of the vertices
of the triangle.
- Construct angles of
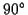 ,
, 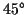 ,
, 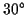 ,
,
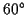 , and if you want a challenge,
, and if you want a challenge, 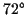 .
.
- Construct a regular pentagon. (A regular pentagon is a five
sided figure all of whose sides and angles are equal.)
- Given a point
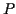 on a circle
on a circle 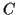 , construct a line through
, construct a line through 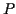 and tangent to
and tangent to 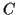 .
.
- Given a circle
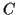 and a point
and a point 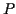 not on
not on 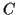 , construct a line
through
, construct a line
through 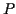 and tangent to
and tangent to 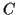 .
.
- Given two circles
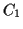 and
and 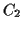 , find lines internally and
externally tangent to both.
, find lines internally and
externally tangent to both.



Next: Algebraic Equivalent
Up: construct
Previous: Some Final Warnings
Zvezdelina Stankova-Frenkel
2000-11-13