Next: Unique and nonunique factorization Up: bamc Previous: bamc

Basic facts

I'll answer half of the title question immediately. For the purposes of this talk, an algebraic number is a complex number which is the root of a polynomial with integer coefficients. An algebraic integer is an algebraic number which is the root of a monic polynomial with integer coefficients. I'll say more about why you should care later. For now, let me just give a bunch of examples to convince you that algebraic numbers crop up all over the place.

A rational number is an algebraic number; a rational number is an algebraic integer if and only if it is an integer. For clarity, I'll refer to the usual integers as the rational integers.
For any rational number , the root of unity $e^{2\pi i p/q}$ satisfies the polynomial , and so is an algebraic integer.
A Gaussian integer, a number of the form , is an algebraic integer.
For any rational number , the numbers $\cos (2\pi p/q)$ and $\sin (2\pi p/q)$ are algebraic integers, and $\tan (2\pi p/q)$ is an algebraic number. Can you explicitly write down polynomials that these are roots of? (These polynomials turn out to have lots of interesting properties.)
Given a recurrence relation $x_{n+k} = a_1 x_{n+k-1} + \cdots + a_k x_n$ with (rational) integer coefficients, all solutions can be expressed in terms of some algebraic integers. For example, the -th Fibonacci number can be written as

$\displaystyle \frac{1}{\sqrt{5}} \left[ \left( \frac{1+\sqrt{-5}}{2} \right)^n - \left( \frac{1 - \sqrt{-5}}{2} \right)^n \right].$
The eigenvalues of a matrix with (rational) integer entries are algebraic integers. This is one way algebraic numbers come up in topology, group theory, algebraic geometry, combinatorics, etc.

Here are some basic facts about algebraic numbers. These may not be obvious at first; I'll mention two ways to prove them in a moment.

The set of algebraic numbers is closed under addition, subtraction, multiplication and division. The set of algebraic integers is closed under addition, subtraction and multiplication, but not division.
The root of a polynomial whose coefficients are algebraic numbers (resp., algebraic integers) is one also.

The first method involves symmetric polynomials, which are interesting enough in their own right that I'll discuss them in some detail.

Theorem 1 Let

be a symmetric polynomial (with integer coefficients) in $x_1, \dots, x_n$ . Then

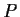
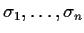
can be expressed as a polynomial (with integer coefficients) in the elementary symmetric functions $\sigma_1, \dots, \sigma_n$ given by

$\displaystyle t^n + \sigma_1 t^{n-1} + \cdots + \sigma_n = (t+x_1)\cdots (t+x_n).$

For example, $\sigma_1 = x_1 + \cdots + x_n$ , $\sigma_2 = \sum_{i<j} x_ix_j$ , and so on. The proof of this is a successive elimination argument of a form quite common in computational algebraic geometry. It's related to something called a ``Gröbner basis''.

Proof. The idea is to deal with the terms of

``from the outside in''. That is, we first deal with terms which are as ``unbalanced'' as possible. We can write

$\displaystyle P = \sum_{a_1\geq \cdots \geq a_n} \sum_{\mathrm{sym}}c_{a_1,\dots,a_n} x_1^{a_1}\cdots x_n^{a_n}.$

We put an ordering on

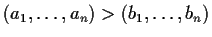
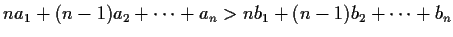
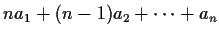
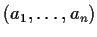
-tuples by saying that $(a_1, \dots, a_n) > (b_1, \dots, b_n)$ if and only if $na_1 + (n-1)a_2 + \cdots + a_n > nb_1 + (n-1)b_2 + \cdots + b_n$ . Now sort the terms in decreasing order by $na_1+(n-1)a_2+\cdots+a_n$ . Choose the biggest term $(a_1, \dots, a_n)$ and notice that the polynomial

$\displaystyle \sigma_1^{a_1-a_2} \cdots \sigma_{n-1}^{a_{n-1}-a_n} \sigma_n^{a_n}$

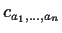
has the same largest term, and the coefficient of that term is 1. So subtract off $c_{a_1,\dots,a_n}$ times this product, and repeat. $\qedsymbol$

I'll demonstrate why this is a useful fact by showing that the product of two algebraic integers is an algebraic integer. Given two algebraic integers which are the roots of the monic polynomials

and

with rational integer coefficients, let $\alpha_1, \dots, \alpha_m$ and $\beta_1, \dots, \beta_n$ be the roots of

and

, respectively. Now consider the polynomial

$\displaystyle \prod_{i=1}^m \prod_{j=1}^n (x - \alpha_i \beta_j).$

Now $\prod_{j=1}^n (x - \alpha_i \beta_j)$ can be viewed as a symmetric polynomial in $\beta_1, \dots, \beta_n$ , if I treat

and $\alpha_i$ as constant. (More precisely, if I look at all terms with a fixed power of

and $\alpha_i$ , these together form a symmetric polynomial in the $\beta_i$ ). By the theorem, this polynomial is a polynomial in the elementary symmetric functions of the $\beta_i$ , which by assumption are integers. So we now have a polynomial in

and $\alpha_i$ with integer coefficients; we now take the product over the $\alpha_i$ and repeat the argument. The second, more modern method, uses some linear algebra. The main idea is that $\alpha$ is an algebraic number if and only if $1, \alpha, \alpha^2, \dots$ lie in a finite dimensional vector space over $\mathbb{Q}$ . So to show that $\alpha \beta$ is algebraic given that $\alpha$ and $\beta$ are, suppose $\alpha$ satisfies a polynomial of degree

and $\beta$ satisfies a polynomial of degree

over $\mathbb{Q}$ . Then all of the products $\alpha^i \beta^j$ lie in the vector space spanned by $\alpha^k \beta^l$ for

. In particular, all of the $(\alpha \beta)^i$ lie in a finite dimensional vector space, so $\alpha \beta$ is algebraic.

Next: Unique and nonunique factorization Up: bamc Previous: bamc

Zvezdelina Stankova-Frenkel 2001-01-14