


Next: Other Possible Rules
Up: Rules
Previous: Rules
The Official Rules
The rules below are actually a little more flexible than the ``official''
rules, but they are easy to understand, and the difference between these
rules and the official rules is explained in the footnote. Here they are:
A construction problem begins with a set of given points, lines, and
circles, and with some desired point, line or circle to construct, based
on the given objects. In the example in Section 1, we
were given two points and the segment between them, and the object of the
construction was to find the point that lies on the segment midway between
the two original points.
Notice that we could reduce the statement above to require that only
certain points be constructed. Obviously, if you want a line, you can
simply require that two different points be found on it, or if you want
a circle you can require that the center and a point on the circle be
found.
At any stage in the construction, you may do any of the following
things to obtain additional points, lines or circles:
- You may draw a straight line of any length through two existing
points. (This means, of course, that the straightedge is as long
as you need it to be, so it is better than a real ruler in that sense.)
- You may find a new point at the intersection of two lines, two
circles, or of a line and a circle. When you are given a segment, of
course, you are given the two points at its ends, so you can certainly
use those.
- You may construct a circle centered at any existing point having
a radius equal to the distance between any two existing points. In
other words, you can set the size of the compass from any two points
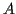 and
and 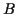 , and then you can move the point of the compass to another
point
, and then you can move the point of the compass to another
point 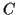 without changing the setting and draw a circle of radius
without changing the setting and draw a circle of radius
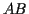 about the point
about the point 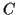 1. (Of course this includes drawing a circle given its
center and a point on the edge--you use the center and the edge to
set the compass size, and then you re-use the center point as the
center of the circle.) As with the straightedge, there is no limit to
the size of a circle that can be drawn, so the mathematical compass is
better than any real one could be.
1. (Of course this includes drawing a circle given its
center and a point on the edge--you use the center and the edge to
set the compass size, and then you re-use the center point as the
center of the circle.) As with the straightedge, there is no limit to
the size of a circle that can be drawn, so the mathematical compass is
better than any real one could be.
- You may choose an arbitrary point on a line, circle,
or on the plane. (And of course you can also choose a point
not on a line or circle as in ``pick any point not on segment
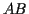 .'')
.'')



Next: Other Possible Rules
Up: Rules
Previous: Rules
Zvezdelina Stankova-Frenkel
2000-11-13