


Next: Diophantine equations
Up: bamc
Previous: Basic facts
It's easier to study algebraic numbers as part of a larger structure than
on their own. So we define a number field to be the smallest set
containing
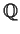 plus some finite set
plus some finite set
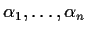 of algebraic
numbers, which is also closed under addition, subtraction, multiplication
and division.
We'll usually denote this number field
of algebraic
numbers, which is also closed under addition, subtraction, multiplication
and division.
We'll usually denote this number field
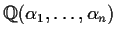 .
We define a ring of integers to be the set of algebraic
integers in a number field.
WARNING: it's not always obvious what the ring of integers in a number
field is. Take the example
.
We define a ring of integers to be the set of algebraic
integers in a number field.
WARNING: it's not always obvious what the ring of integers in a number
field is. Take the example
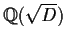 (
(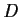 positive or negative).
If
positive or negative).
If
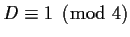 , then
, then
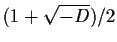 is an algebraic integer; more generally, the integers
in the number field are
is an algebraic integer; more generally, the integers
in the number field are
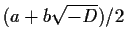 for
for 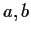 rational integers of the
same parity. If
rational integers of the
same parity. If
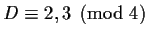 , then the only integers in
the number field are the obvious ones
, then the only integers in
the number field are the obvious ones
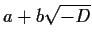 for
for 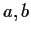 rational integers.
One nice property about the rational integers is unique factorization.
Is unique factorization true for other rings of integers? Sometimes yes,
sometimes no.
To make that precise, we'll need some more definitions.
define a unit to be an algebraic integer whose reciprocal is
also an algebraic integer. (For example, roots of unity are units, but there
are other units too; we'll see some later.)
We call an element
rational integers.
One nice property about the rational integers is unique factorization.
Is unique factorization true for other rings of integers? Sometimes yes,
sometimes no.
To make that precise, we'll need some more definitions.
define a unit to be an algebraic integer whose reciprocal is
also an algebraic integer. (For example, roots of unity are units, but there
are other units too; we'll see some later.)
We call an element 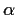 of a ring of integers irreducible if
whenever you write
of a ring of integers irreducible if
whenever you write
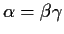 as the product of two elements
of the ring, one of
as the product of two elements
of the ring, one of 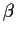 or
or 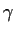 is a unit. (I didn't say ``prime''
because I'm saving that word for later).
We say a ring of integers has unique factorization if whenever
an element of a ring of integers is expressed as a product of irreducible
elements, that expression is unique up to changing the order and multiplying
by units.
For example, the Gaussian integers have unique factorization,
because they admit an analogue of the Euclidean division algorithm.
is a unit. (I didn't say ``prime''
because I'm saving that word for later).
We say a ring of integers has unique factorization if whenever
an element of a ring of integers is expressed as a product of irreducible
elements, that expression is unique up to changing the order and multiplying
by units.
For example, the Gaussian integers have unique factorization,
because they admit an analogue of the Euclidean division algorithm.
Theorem 2
Given Gaussian integers
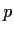
and
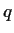
with
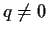
,
there exist Gaussian integers
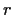
and
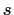
with
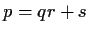
and
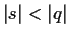
.
Proof.
Draw the square with vertices
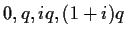
. Then
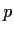
is congruent to a Gaussian integer
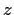
inside (or on the boundary of) the square.
Also, the open discs of radius
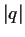
centered at
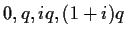
cover
the square completely, so
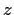
is within
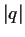
of one corner of the square,
say
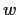
. Now take
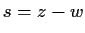
; then
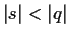
and
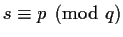
,
so we can set
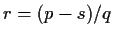
and we're done.

Corollary 1
Every (rational) prime congruent to 1 modulo 4 is the sum of two squares;
moreover, this expression is unique up to order and signs.
Proof.
If
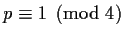
, then there exist
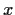
and
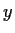
such that
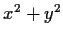
is divisible by
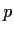
but not by
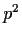
. Apply the Euclidean algorithm
in the Gaussian integers (left for you to write down!) to
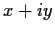
and
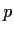
;
the result will be a Gaussian integer
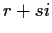
with
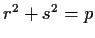
. Uniqueness
is also left to you.

EXERCISE: Find some other rings of integers which have unique factorization.
(For starters, try
![$ \mathbb{Z}[\sqrt{-2}]$](img76.gif) and
and
![$ \mathbb{Z}[(1+\sqrt{-3})/2]$](img77.gif) .
On the other hand, consider this example in
.
On the other hand, consider this example in
![$ \mathbb{Z}[\sqrt{-5}]$](img78.gif) :
None of 2, 3, or
:
None of 2, 3, or
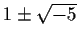 can be written as a nontrivial
product of two elements of
can be written as a nontrivial
product of two elements of
![$ \mathbb{Z}[\sqrt{-5}]$](img78.gif) , so this ring doesn't have
unique factorization. What to do?
Kummer realized that one could find an algebraic integer in a bigger ring
that would allow you to break up such problem factorizations. (For example,
if we toss in
, so this ring doesn't have
unique factorization. What to do?
Kummer realized that one could find an algebraic integer in a bigger ring
that would allow you to break up such problem factorizations. (For example,
if we toss in 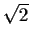 , then it divides both
, then it divides both
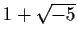 and
and 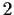 .)
However, it turns out that it's a little better to work not
with these ``ideal numbers'', as Kummer called them, but with the collection
of their multiples.
Definition: an ideal in a ring of integers
.)
However, it turns out that it's a little better to work not
with these ``ideal numbers'', as Kummer called them, but with the collection
of their multiples.
Definition: an ideal in a ring of integers 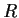 is a subset
is a subset
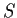 such that
such that
- for
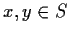 ,
, 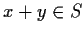 ;
;
- if
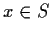 and
and 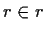 , then
, then 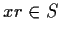 .
.
Example: If
 , then an ideal is an arithmetic progression containing 0.
More general example: the principal ideal generated by
, then an ideal is an arithmetic progression containing 0.
More general example: the principal ideal generated by 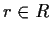 consists
of all multiples of
consists
of all multiples of 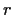 . But not all ideals have this form!
Because of the way an ideal is defined, we can work ``modulo'' an ideal, that is,
it makes sense to write
. But not all ideals have this form!
Because of the way an ideal is defined, we can work ``modulo'' an ideal, that is,
it makes sense to write
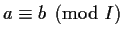 because this equivalence respects
addition and multiplication. If
because this equivalence respects
addition and multiplication. If 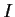 is nonzero, then the number of equivalence
classes modulo
is nonzero, then the number of equivalence
classes modulo 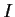 is finite; we call this number the norm of the ideal.
An ideal
is finite; we call this number the norm of the ideal.
An ideal 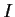 is prime if
is prime if 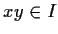 implies
implies 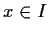 or
or 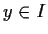 . For
example, if
. For
example, if
 and
and 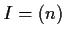 , then
, then 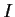 is prime if and only if
is prime if and only if 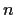 is prime. In general, if
is prime. In general, if 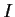 has prime norm, it is a prime ideal, but the converse
is not true; we only know that
has prime norm, it is a prime ideal, but the converse
is not true; we only know that 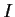 has prime power norm. For example, the
ideal
has prime power norm. For example, the
ideal 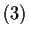 in
in
![$ \mathbb{Z}[i]$](img100.gif) is prime, but its norm is 9.
The arithmetic on
is prime, but its norm is 9.
The arithmetic on
![$ \mathbb{Z}[i]/(3)$](img101.gif) is not the same as on
is not the same as on
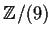 , though!
The main distinction is that in
, though!
The main distinction is that in
![$ \mathbb{Z}[i]/(3)$](img101.gif) ,
everything not congruent to 0 mod
,
everything not congruent to 0 mod 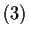 has a multiplicative inverse. (Thus
has a multiplicative inverse. (Thus
![$ \mathbb{Z}[i]/(3)$](img101.gif) is an example of a
finite field.)
The big theorem about prime ideals is the recovery of unique
factorization.
is an example of a
finite field.)
The big theorem about prime ideals is the recovery of unique
factorization.
Theorem 3
Every nonzero ideal in a ring of integers has a unique prime factorization.
Corollary 2
If every ideal of a ring of integers
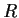
is principal, then
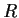
has unique
factorization. (Note: the converse is also true.)
Two ideals 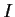 and
and 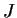 in the ring of integers
in the ring of integers 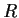 of a number field
of a number field 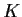 are equivalent
if there exists
are equivalent
if there exists 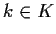 such
that
such
that 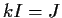 . (Note that
. (Note that 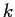 need not lie in
need not lie in 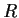 . If you prefer a definition
within
. If you prefer a definition
within 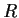 :
: 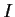 and
and 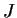 are equivalent if there exist nonzero
are equivalent if there exist nonzero 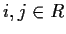 such that
such that 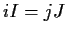 .)
This equivalence is respected by multiplication.
.)
This equivalence is respected by multiplication.
Theorem 4 (Minkowski)
The number of equivalence classes of ideals in a ring of integers is finite.
This number is called the class number of the number field.
Theorem 5 (Gauss)
For
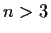
not divisible by 4,
the number of primitive (having no common factor)
triples
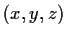
of integers such that
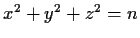
is equal to
12 times the class number of
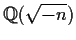
if
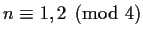
,
or 24 times the class number of
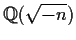
if
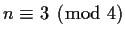
.
Note: Gauss didn't express this theorem in terms of number fields,
but in terms of binary quadratic forms
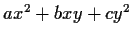 whose discriminant
whose discriminant
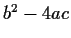 equals
equals 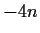 , if
, if
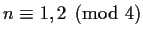 ,
or
,
or 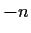 , if
, if
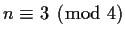 . Two forms are equivalent if you can get
from one to the other by making a variable substitution of the form
. Two forms are equivalent if you can get
from one to the other by making a variable substitution of the form
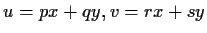 where
where 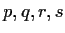 are integers with
are integers with 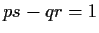 .
EXERCISE: Prove that
the number of equivalence classes of forms equals the class number
of
.
EXERCISE: Prove that
the number of equivalence classes of forms equals the class number
of
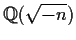 .
.



Next: Diophantine equations
Up: bamc
Previous: Basic facts
Zvezdelina Stankova-Frenkel
2001-01-14