


Next: Linear recursive sequences
Up: Linear recursive sequences
Previous: Sequences
Recursive definitions
An alternative way to describe a sequence is to list a few terms
and to give a rule for computing the rest of the sequence.
Our example (1) above can be described by
the starting value 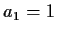 and the rule
and the rule
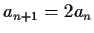 for integers
for integers 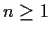 .
Starting from
.
Starting from 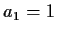 , the rule implies that
, the rule implies that
and so on; each term in the sequence can be computed recursively
in terms of the terms previously computed.
A rule such as this giving the next term in terms of earlier terms
is also called a recurrence relation (or simply recurrence).
Zvezdelina Stankova-Frenkel
2000-09-20
![]() and the rule
and the rule
![]() for integers
for integers ![]() .
Starting from
.
Starting from ![]() , the rule implies that
, the rule implies that